У каждого учителя в запасе всегда есть множество разных штучек которые он использует в своей работе. Какие-то постоянно, какие-то в зависимости от класса и ситуации, от каких-то использует частички, а некоторые он просто хранит потому, что интуитивно видит в них мощный потенциал, но не решил пока как и когда использовать. Именно их он начинает осмысливать и искать место и “время выстрела” в своей работе. Любой учитель анализирует удачи и неудачи своих учеников через поиск проблемных точек и искать пути их сглаживания.
Одной из объединяющих идей сообщества SIGNUM является Desmos. Педагоги (и не только) активно занимаются переводом активностей англоязычных авторов и их адаптацией, в том числе и для российских школ. Изучая активности Desmos и их место в школьном образовании мы делаем для себя открытия не только в инструментальном плане, но и в методическом, собирая те самые штучки. Работая с переводами мы увидели, что подходы американских учителей отличаются от наших, здесь можно развить дискуссию, разобрать все за и против, но далее о другом.
В списке активностей для перевода, была активность “Properties of Equality using Algebra Tiles” что в машинном перевода означает “Свойства равенства с использованием плиток алгебры”. К удивлению перевод активности ясности не внес. “Плитки алгебры” - совершенно не известное сочетание кроме того непонятно было как ее использовать и к какому разделу математики отнести. Интерес мотивировал разобраться.
Что это?
“Плитки алгебры - это математические манипуляторы, которые позволяют учащимся лучше понять способы алгебраического мышления и концепции алгебры.”
“В математическом образовании , манипулятивный является объектом , который спроектирован таким образом, что ученик может воспринимать некоторые математические понятия, манипулируя его. Использование манипуляторов дает детям возможность изучать концепции на основе практического опыта, соответствующего их развитию. Математические манипуляторы часто используются на первом этапе обучения математическим понятиям - конкретному представлению.”
Так что это?
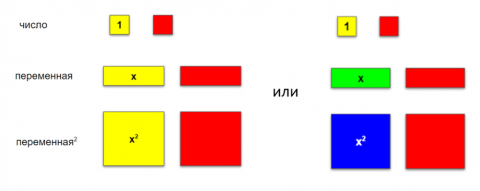
Это плитки разной формы (малый и большой квадрат, прямоугольник) и разного цвета. Цвет обозначает знак. Например, желтый малый квадрат это 1, красный это -1. Причем, эти цвета на одной плитке, одной стороны желтый, с другой стороны красный, т.е. переворот плитки означает смену знака. В продаже есть наборы Algebra Tiles, но их без проблем можно сделать их магнитной и цветной бумаги бумаги (для магнитной доски). Цвета могут быть разные, но важно обозначение отрицательного одним цветом - обычно красным. У меня на это ушло 20 мин, два набора цветной самоклеющейся бумаги и три листа фотобумаги на магнитной основе.
Сумма противоположных чисел равна нулю = две плитки одной формы но разного цвета образуют нулевую пару, т.е. их можно убрать.

Понятие очень легко вошло в урок при решении систем уравнений способом сложения, например: “Найдите нулевую пару, создайте нулевую пару”.
Размеры плиток подбираются так, чтобы их можно было сложить в квадрат, через который работает умножение.
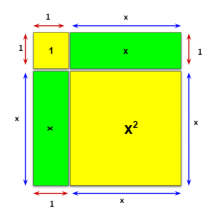
Плитки алгебры это манипуляция с перекладыванием плиток под определенные условия.
Зачем?
Методика использования плиток алгебры очень подробно описана в коротких видео на сайте Daniel Kaufmann и на youtube (субтитры /перевести/ русский)
Несколько примеров:
Действия с рациональными числами
4 желтых и 7 красных = 4 нулевые пары и 3 красных, т.е. -3
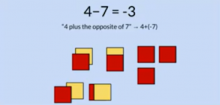
3 - (-2) по опыту сложная для понимания детьми ситуация
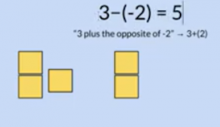
Что в плитках? 3 желтые, -2 красные, НО -(-2) это противоположность красного, т.е. желтое. В итоге 5 желтых плиток.
Разложение трехчлена на множители
Помимо настольной (для доски) версии плиток есть еще онлайн-игра “Algebra Tiles”. При решении уравнений надо не только вписать число в ответ. Сначала правильно разложить плитки по исходному уравнению, после этого откроется окно для записи ответа, но мало вписать ответ, задание будет выполнено если и решение на плитках выполнено верно.

А зачем это?
Это совершенно иное восприятие процесса изучения математики, больше визуализации, меньше научности (сухих правил), как следствие, меньше страха у детей. Это реальное представление процесса. Ну и конечно - игра.
Набор моих учительских штучек пополнился...


