Темой нашего сегодняшнего практикума будет моделирование движения объектов под действием силы упругости. Это позволит нам решать самые разнообразные учебные и проектные задачи, ведь сила упругости - одна из главных сил в окружающем мире. В частности мы сумеем воспроизвести в компьютерной игре на базе Scratch поведение двух или нескольких бильярдных шаров при столкновении, либо сделать симулятор робофутбола, в котором лёгкий мяч будет правдоподобным образом отскакивать от тяжелого робота, когда тот подъезжает к нему с некоторой скоростью. Кроме того, мы научимся учитывать и другие силы - трение качения, сопротивление воздуха. Наша физическая модель превратится в интересный инструмент, позволяющий проводить виртуальные "физические опыты" на экране компьютера.
В конце данного занятия мы получим готовую компьютерную модель упругого взаимодействия объектов, которую можно будет модифицировать для того или иного частного применения. Определим основные этапы нашей работы:
- подготовка всего необходимого;
- моделирование гармонических (упругих) колебаний объекта, двигающего по прямой (в одномерном пространстве);
- учёт сил трения (затухающие колебания);
- преобразование модели в модель движения по инерции с повторяющимися упругими столкновениями;
- моделирование столкновений двух круглых объектов на плоскости (в двухмерном пространстве) с дальнейшим движением их по инерции;
- в перспективе - модель движения на горизонтальной или наклонной плоскости группы круглых объектов, имеющих разный размер, массу, скорость, коэффициент упругости, коэффициент трения и аэродинамическое сопротивление с обсчётом множественных, в том числе одновременных столкновений.
Конечно же нам придётся разбивать каждую подзадачу на ещё более мелкие. Будем двигаться по шагам. Кроме того, первые базовые задачи удобнее решать в среде Scratch, а вот для работы не с двумя объектами, а со множеством потребуется более совершенная среда программирования - Snap4arduino.
Создание модели множественных столкновений на первый взгляд воспринимается невероятно сложным, однако принцип разбиения задачи на составные части позволяет собрать итоговый проект буквально "по кусочкам", а каждая отдельная подзадача сама по себе не так уж сложна.
Подготовка
Мы будем использовать визуальную среду Scratch3. Онлайн-редактор можно открыть по следующей ссылке.
https://scratch.mit.edu/projects/editor/
Тот, кому удобнее будет работать с оффлайн-версией Scratch, может загрузить инсталляционный пакет для используемой операционной системы и установить программу на свой компьютер.
https://scratch.mit.edu/download
Этап 1. Воссоздаём гармонические колебания и рисуем синусоиду
Гармонические колебания в пространстве — колебания, при которых положение объекта изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
ru.wikipedia.org/wiki/Гармонические_колебания
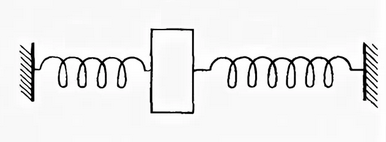
Для нас существенным является то, что тело совершает гармонические колебания под действием силы, пропорциональной смещению от положения равновесия и направленной противоположно этому смещению. Типичный пример - некий груз, колеблющийся между двумя пружинами.
Давайте смоделируем такую систему в Scratch. Создайте новый проект, удалите из него спрайт кота, добавьте подходящий новый спрайт. Пусть это будет "Ball" из библиотеки спрайтов. Кроме того, в библиотеке фонов есть полезное для нас изображение с именем "Xy-grid", установите этот рисунок как фон, выбрав объект Сцена.
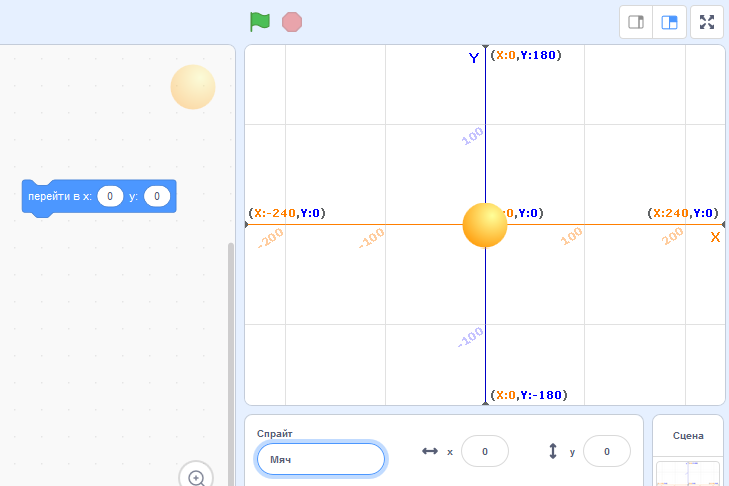
Выберите снова спрайт "Ball", переместите его в центр экрана при помощи блока "перейти в x: (0) y: (0)". Переименуйте, назвав "Мяч".
Для наглядности и гибкости проекта создайте переменные со следующими именами: "скорость", "ускорение", "масса", "жёсткость" и "деформация". Все они должны быть локальными, при создании укажите опцию "только для этого спрайта". Это позволит в нам в будущем иметь в проекте несколько спрайтов, работающих сходным образом.
По умолчанию выставлен маркер отображения значения переменной на сцене. Можно увидеть, что каждая переменная имеет префикс "Мяч" в названии.
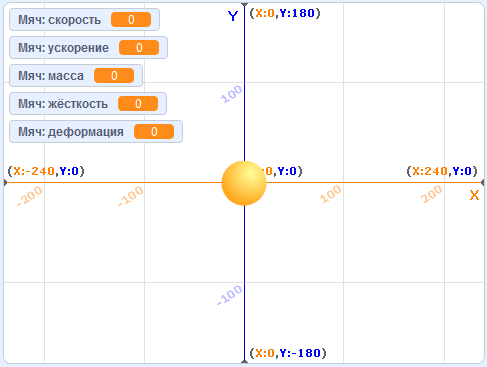
Следует отметить, что характеристики "жёсткость" и "деформация" относятся не к самому мячу в нашей модели, а к тем условным "пружинам", на которых мяч "подвешен". Произведение жёсткости на деформацию пружины (пружин) определяет силу, которая действует на мяч.
Соберите следующий скрипт.
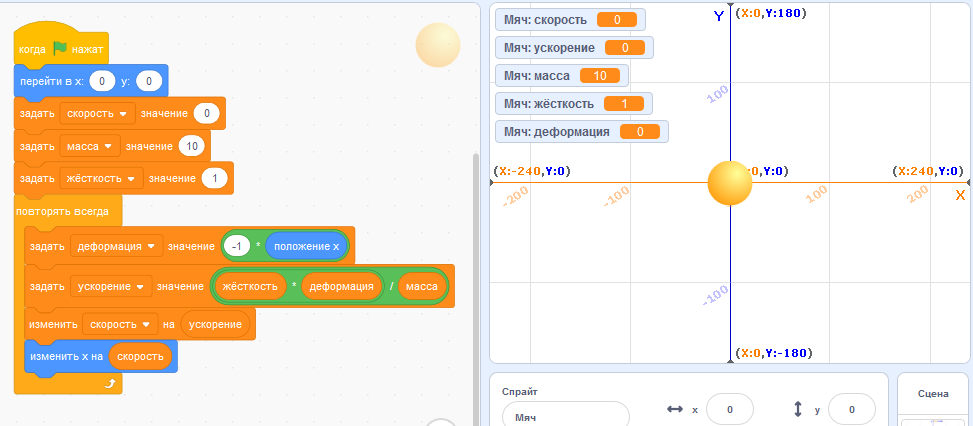
Обратите внимание, что последние два блока скрипта - не "задать", а "изменить".
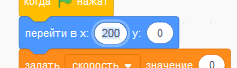
Запустите программу. Что произошло? Ровно ничего, и это вполне естественно. Мяч находится в точке равновесия и его начальная скорость равна нулю, поэтому он и не стал двигаться. Поменяйте начальное положение мяча, отредактировав значение X в блоке "перейти в...".
Запустите программу снова. Теперь мяч начал колебаться влево-вправо. Как видите, крайние точки его траектории это 200 и -200. Для того, чтобы понаблюдать за процессом повнимательнее, увеличьте массу мяча в 10 раз. Теперь можно успевать отслеживать изменения параметров во время колебаний.
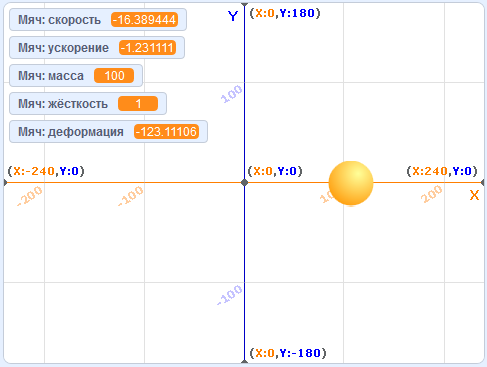
Однако картина может быть ещё нагляднее, если заставить мяч рисовать график своих перемещений. Сделать это несложно. Понадобятся блоки из расширения "Перо", которое можно добавить кнопкой в левом нижнем углу экрана.
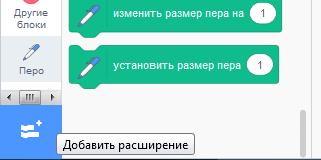
Необходимо доработать скрипт таким образом, чтобы менялась не только позиция X, но и позиция Y. Мы будем использовать для этого свой собственный блок
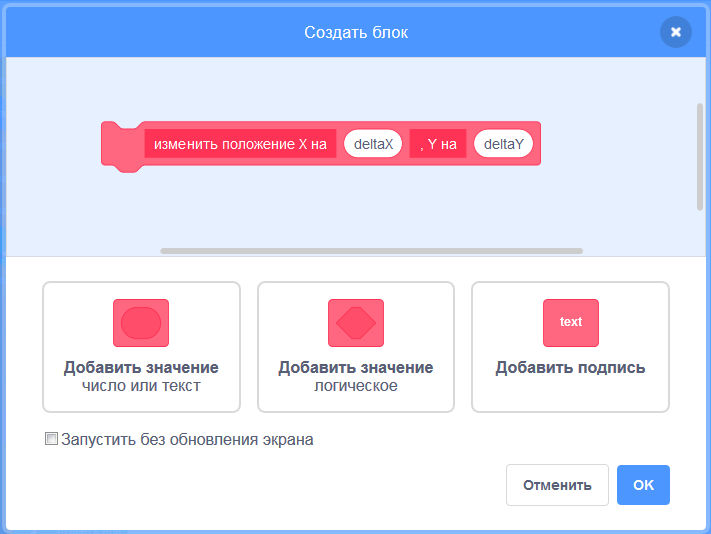
"изменить положение X на ( ) , Y на ( )". Создайте его.
В разделе "Другие блоки" палитры скриптов нажмите на кнопку "Создать блок". Появится окно, в котором надо будет отредактировать название, добавить два значения и ещё одну подпись, чтобы получилось как на рисунке.
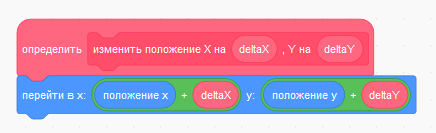
К "шапочке" (определению) блока добавьте скрипт:
Полный набор скриптов для спрайта "Мяч" теперь выглядит так.
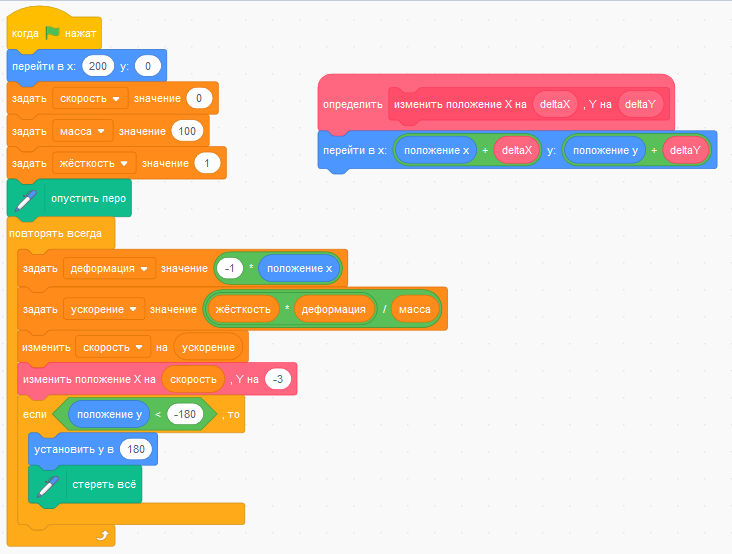
Значения переменных, отображаемые на сцене, нам будут мешать. Снимите маркеры, чтобы спрятать их.
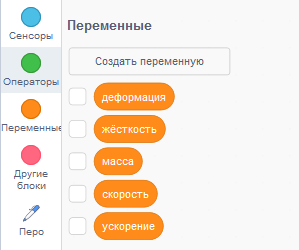
Запустите программу. Теперь мяч перемещается сверху вниз во время колебаний, и за ним остаётся след синусоидальной формы.
Сохраните проект, теперь его можно использовать как шаблон для создания новых, более сложных.
Можно было бы уже перейти к следующему шагу, но очень уж интересно узнать, по какому закону меняются значения переменных "скорость" и "ускорение" во время движения мяча. Сделаем пробную модификацию программы, чтобы видеть ещё два графика. Рисовать эти графики будут два дополнительных спрайта.
Создайте две глобальных переменных (которые будут доступны всем спрайтам) с именами "показатель1" и "показатель2". Добавьте в скрипт мяча блоки, задающие значения этих переменных на основе скорости и ускорения мяча.
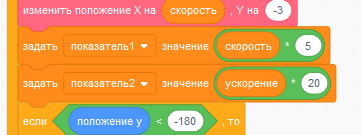
Добавьте новый спрайт с костюмом стрелки, отредактируйте, поменяв цвет и положение центральной точки спрайта. Соберите скрипт.
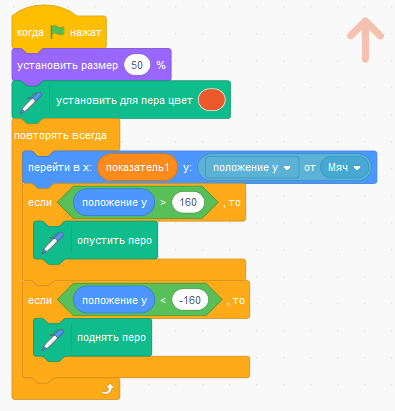
Красная стрелка будет рисовать красным пером график изменения значения переменной "показатель1".
Сделайте дубль этого спрайта, отредактируйте цвет стрелки и цвет пера. Замените переменную "показатель1" переменной "показатель2".
Запустите проект. Теперь на сцене сразу три графика - перемещения, скорости и ускорения. Как видите, все они имеют синусоидальную форму. При этом любопытно то, что в нашей программе не используются функции синуса или косинуса, вычисления происходят за счёт интегрирования (суммирования значений).
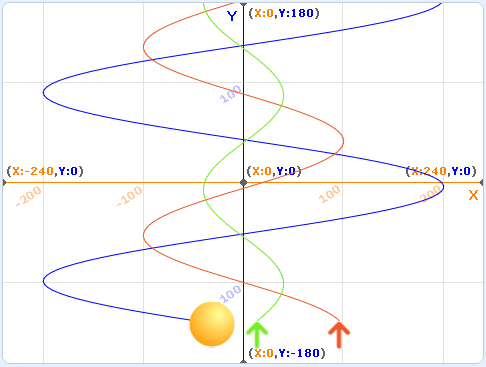
Файл с готовым проектом: этап1.sb3
Этап 2. Учитываем силы трения и сопротивления
Колебания мячика в нашей модели незатухающие, они происходят непрерывно с одной и той же амплитудой. Добавим реалистичности в наш проект, будем непрерывно уменьшать скорость движения в соответствии с действием сил трения и сопротивления среды, в которой перемещается мяч.
Можно уменьшать скорость движения тремя разными способами:
- делать её меньше по модулю на некоторую фиксированную величину (что соответствует трению покоя или возникновению остаточной деформации пружины, например);
- уменьшать её пропорционально скорости движения (так называемое "вязкое трение");
- уменьшать её пропорционально квадрату скорости движения (аэродинамическое сопротивление воздуха).
Мы введём три коэффициента для каждого вида сопротивления, чтобы наша модель была универсальной. Если все три коэффициента равны нулю, происходят незатухающие колебания.
Откройте версию проекта, в которой существует лишь один спрайт - "Мяч". Добавьте три локальных (только для этого спрайта) переменных - "к0", "к1" и "к2". Это коэффициенты трёх видов сопротивления.
Наш проект разрастается, для сохранения наглядности разобьём его на блоки с осмысленными названиями. Теперь набор скриптов должен выглядеть так.
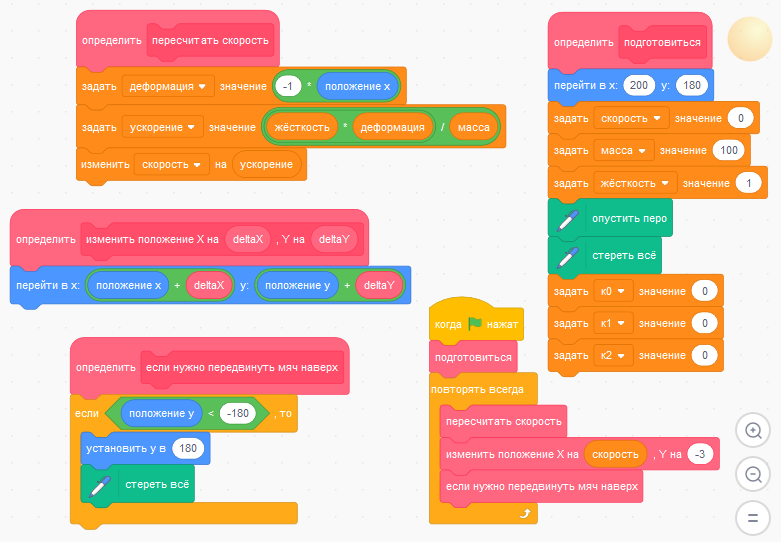
Запустите проект, чтобы проверить, что он работает и в таком виде.
Добавьте новый блок "учесть сопротивление" и поменяйте значения "к0", "к1" и "к2". Изменившаяся часть набора скриптов:
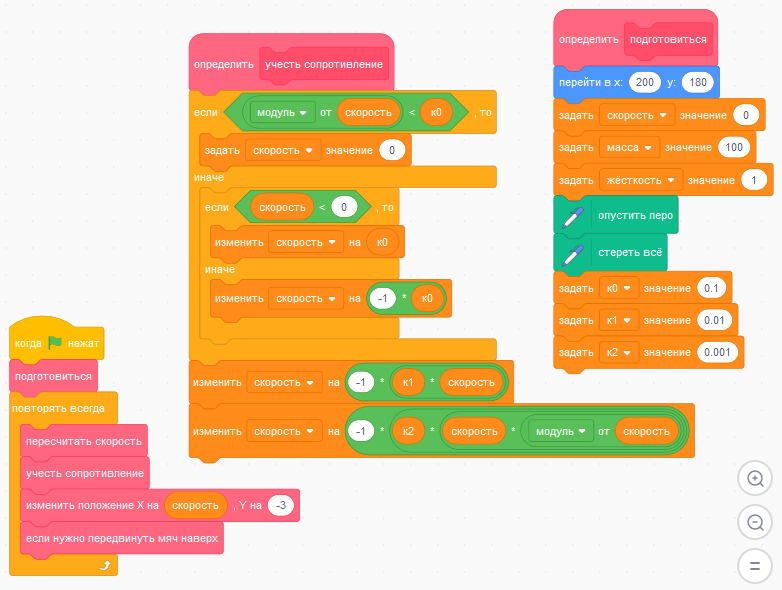
Запустите программу. Поэкспериментируйте с разными значениями коэффициентов, проверьте, как выглядят колебания мяча, если выставить два коэффициента в ноль и оставить лишь один из видов сопротивления движению.
Обратите внимание, что период колебаний мяча не зависит от их амплитуды.
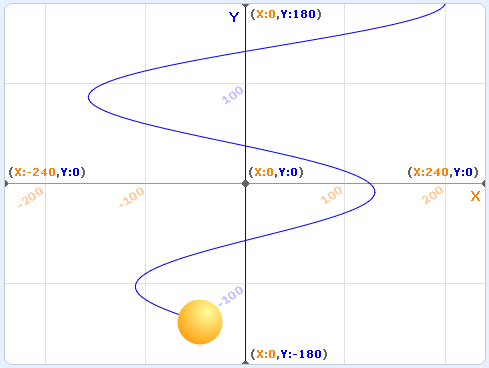
Файл с готовым проектом: этап2.sb3
Этап 3. Свободное движение по инерции с повторяющимися упругими столкновениями
Столкновение одного тела с другим часто рассматривают как "удар", то есть явление настолько короткое, что его длительностью можно пренебречь. При этом для вычисления конечных скоростей и направлений движения тел после удара используют специальные методы расчёта.
Но поскольку мы уже создали модель упругого взаимодействия, а компьютер производит все вычисления крайне быстро, нам несложно будет самостоятельно решить задачу моделирования столкновения двух тел. Причём мы не будем упрощать картину и считать время взаимодействия тел равным нулю.
Модифицируем нашу компьютерную модель таким образом, чтобы появилась фаза свободного движения между столкновениями с правой и левой границей свободного пространства. Нам понадобятся переменные "правГраница" и "левГраница". Начальное положение мяча - посередине, мяч при старте программы имеет некоторую скорость.
Существующие коэффициенты "к0", "к1" и "к2" будем использовать для учёта возможного сопротивления движению во время свободной фазы. Давайте для начала условимся, что фаза свободного движения проходит без какого-либо трения и без сопротивления воздуха. Во время контакта мяча с левой или правой границей будем использовать "кПрав0", "кПрав1", "кПрав2", "кЛев0", "кЛев1" и "кЛев2". Кроме того, жёсткость левой и правой границы может быть разной, поэтому теперь у нас будет две переменной вместо одной: "жёсткостьПрав" и "жёсткостьЛев".
Создайте все новые переменные, они должны быть локальными. Теперь необходимо доработать набор скриптов спрайта "Мяч".
Отредактируйте определение блока "учесть сопротивление" так, чтобы использовалось три параметра.
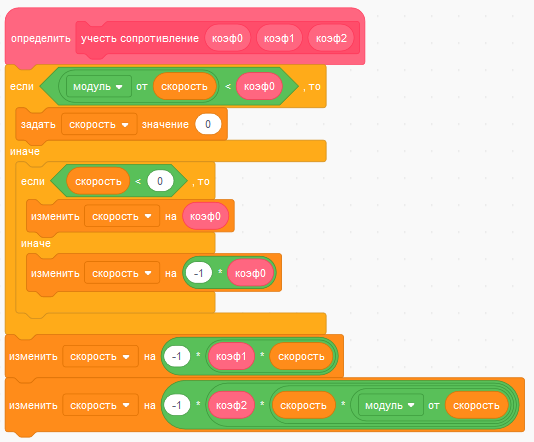
Переименуйте блок "пересчитать скорость", дайте ему название "пересчитать скорость и учесть сопротивление". Доработайте скрипт.
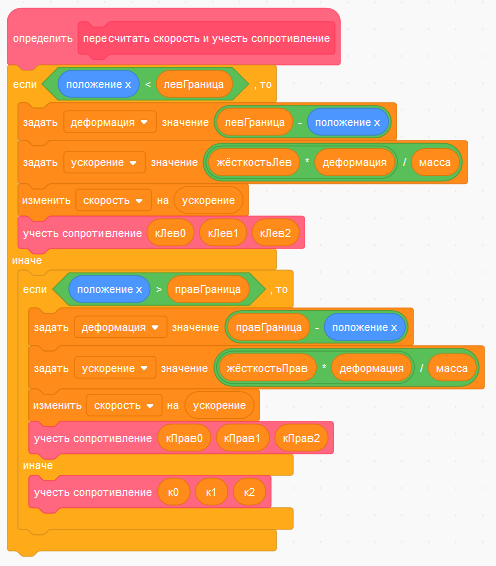
Остальной набор скриптов:
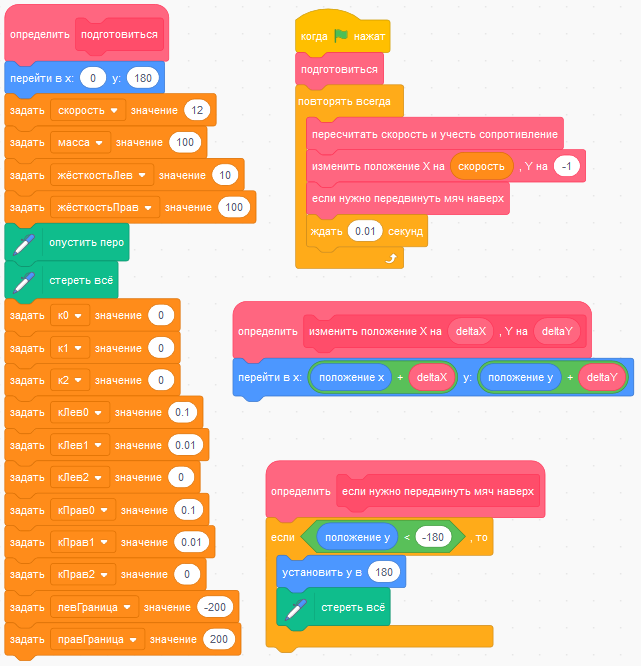
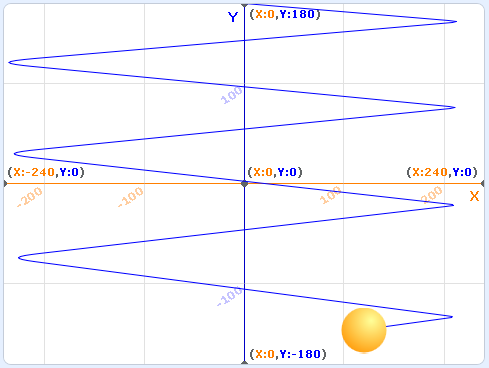
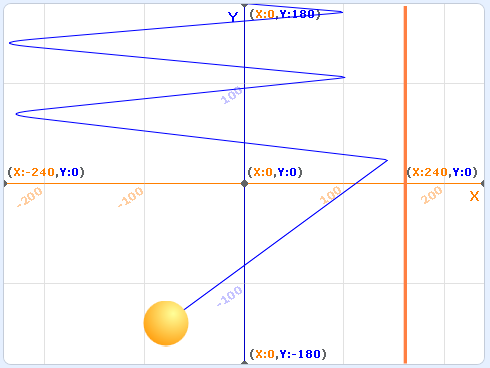
Запустите программу. График движения мяча влево-вправо теперь выглядит как пила, и можно заметить, что отскоки от правой границы происходят резче, чем от левой.
Файл с готовым проектом: этап3.sb3
Этап 4. Изменение скорости мяча при столкновении с движущимся массивным препятствием
Мы вплотную приблизились к решению более сложной задачи - моделированию отскока от движущегося объекта. И любопытно то, что скрипт, обеспечивающий перемещение мяча, для этого даже не придётся менять, он практически полностью готов!
Единственное дополнение, которое необходимо будет внести, это динамическое изменение расположения правой границы в ходе работы программы. Давайте добавим новый спрайт, который и будет изображать подвижную правую границу.
Создайте спрайт с помощью инструмента "Нарисовать".
Костюмом этого спрайта должна быть тонкая вертикальная линия от верхнего до нижнего края поля редактирования. Её можно нарисовать, например, инструментом "Прямоугольник" с нулевой толщиной контура.
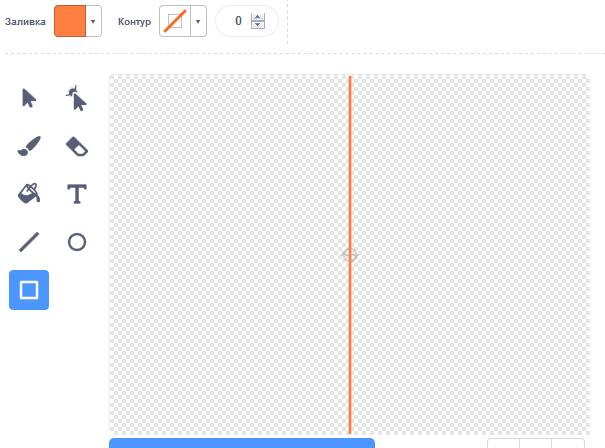
При помощи инструмента "Выбрать" можно поменять ширину и высоту линии, а также поместить её в центр поля редактирования. Под названием костюма - информация о ширине и высоте изображения. Наша линия имеет ширину 4 пикселя.
Дайте спрайту название "препятствие", переключитесь на вкладку "Код" и создайте скрипт. Мы будем двигать линию влево и вправо перемещением мыши.
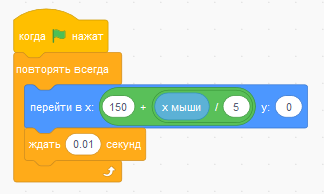
Ширина линии 4 пикселя, но нам надо знать и ширину мяча, чтобы определить размер области свободного перемещения.
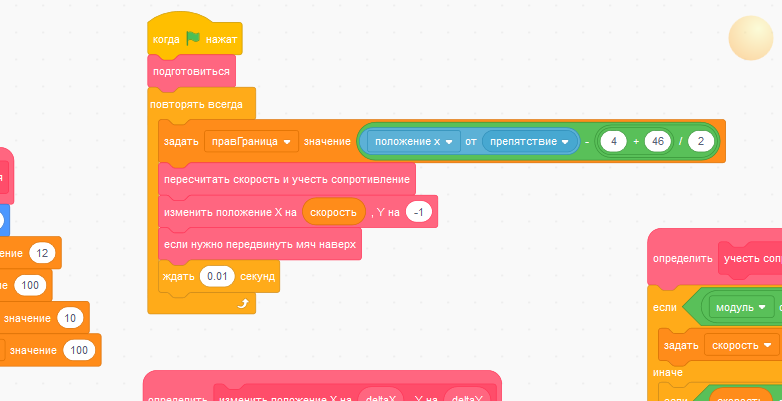
Осталось добавить в основной скрипт мяча одну строку. Числа 4 и 46 обозначают ширину линии и ширину мяча.

Добавьте этот блок в основной скрипт спрайта "Мяч". Теперь скрипт выглядит так.
Запустите программу, проверьте, что будет происходить, если в момент касания отодвигать препятствие от мяча, или напротив, двигать навстречу.
Следует добавить, в данном случае импульс мяча при столкновении никак не меняет скорости движения препятствия. В реальной жизни это соответствовало бы ситуации, когда масса мяча несопоставимо меньше массы препятствия.
В этом проекте нет никакого целенаправленного измерения скорости движения препятствия и использования замеренной скорости препятствия для расчёта скорости движения мяча после столкновения. Тем не менее, как можно заметить, итоговая скорость мяча складывается из его начальной скорости и скорости движения препятствия в момент столкновения.
Вы по-прежнему можете менять коэффициенты, определяющие потери скорости при столкновениях и перемещениях мяча. Например, можно сделать так, чтобы отскок мяча от препятствия сопровождался значительной потерей скорости, как будто бы мяч ударился о какой-то не очень упругий предмет. В этом случае придётся всё время "бить" по мячу, чтобы движение продолжалось. Получится своего рода игра на ловкость. Поэкспериментируйте с разными значениями, в том числе попробуйте увеличить трение во время свободной фазы перемещения.
Файл с готовым проектом: этап4.sb3
Этап 5. Столкновение двух движущихся объектов на плоскости
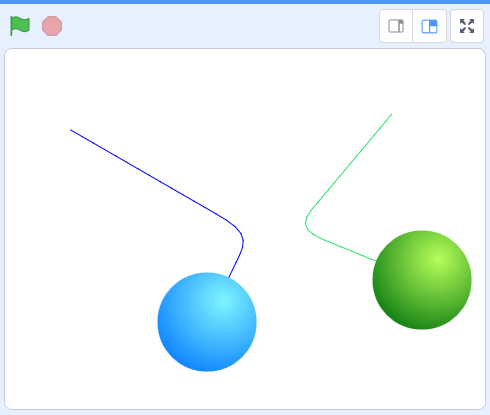
В этом проекте мы будем наблюдать за траекторией движения двух мячей, хаотично катающихся по прямоугольной области сцены в разных направлениях. Мячи будут отскакивать от её границ под действием сил упругости, периодически сталкиваться друг с другом и отскакивать с изменением скорости и направления движения.
Для сохранения наглядности не будем перегружать проект подробностями. В частности, столкновения мячей со стенками и друг с другом будут абсолютно упругими, мы будем учитывать лишь небольшое вязкое трение при свободном перемещении мячей.
Нам понадобится большое количество второстепенных переменных для расчётов. В целом будет проще начать "с чистого листа".
Создайте в среде Scratch новый проект, удалите спрайт кота. Добавьте уже знакомый нам спрайт "Ball". Нам надо будет отредактировать его костюмы.
Удалите все костюмы, кроме синего и зелёного ("ball-b" и "ball-d"). Для упрощения расчётов воспользуемся маленькой хитростью: если сделать размер изображения равным 100x100 пикселей, тогда не придётся пересчитывать проценты в пиксели. Блок "Размер", возвращающий масштаб отображения спрайта, можно будет использовать как диаметр мяча.
Увеличьте размер костюма "ball-b" инструментом "выбор" так, чтобы он стал равен 100x100. Затем передвиньте костюм в центр. В графическом редакторе Scratch3 сделать это легко: разработчики позаботились о том, чтобы изображение "прилипало" к центральной точке.
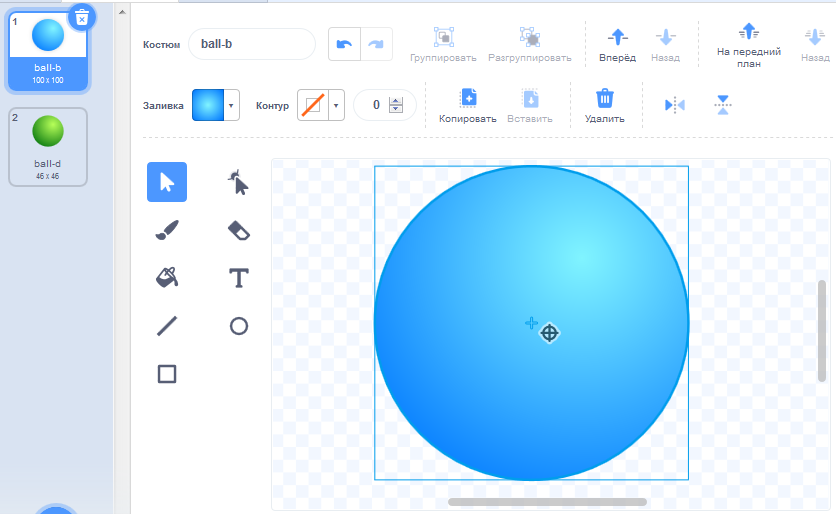
Повторите операцию для зелёного костюма "ball-d". Теперь оба костюма имеют размер 100x100.
У нас будет два мяча - синий и зелёный, каждый мяч будет использовать свой собственный костюм. Один спрайт будет называться "Синий", второй - "Зелёный". Эти названия будут фигурировать в скриптах проекта. Сделайте дубль спрайта мяча, переименуйте оба спрайта, выберите им костюмы.
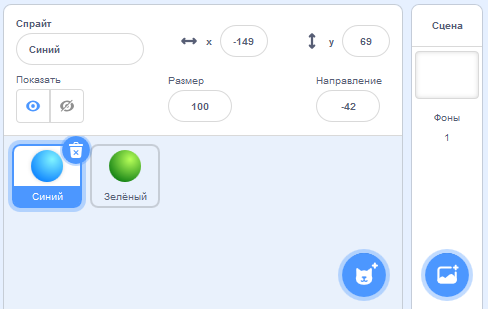
Вначале мы создадим все скрипты для спрайта "Синий", а затем сдублируем их в спрайт "Зелёный" и немножко подправим.
Первым делом необходимо создать набор переменных, которые потребуются нам для расчётов. Очень важно, чтобы все переменные были локальными ("только для этого спрайта"), в противном случае проект будет работать неправильно, и будет сложно понять, почему.
Создайте локальные переменные "масса", "скорость", "sin_Dir", "cos_Dir", "dfrm", "dir_to_object", "dX", "dY", "vX", "vY" и "tmp".
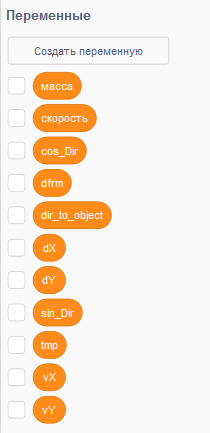
Ниже приведены необходимые скрипты, которые следует создать. Для подробного объяснения, как они работают, потребовалось бы много времени. Укажем лишь, что в программе осуществляется пересчёт линейной скорости и направления движения мяча в горизонтальную и вертикальную составляющую, а затем обратно. Кроме того, можно менять масштаб отображения спрайта и регулировать тем самым его условную массу (при масштабе 100 масса равна единице).
При возникновении проблем рекомендуется отлаживать программу по частям. Например, можно отключить скрипт, отвечающий за проверку столкновений с зелёным мячом. В этом случае синий будет игнорировать наличие другого мяча и отскакивать лишь от границ сцены (либо от границ меньшей области на сцене, если мы захотим). Удобнее работать так: первым делом создать все пользовательские блоки с пустыми поначалу определениями, а затем добавлять скрипты, "подклеивая" и к "шапочкам" (заголовкам). Неважно, что тот или иной блок ещё "пустой", скрипт с его использованием уже можно собирать.

Основной скрипт:
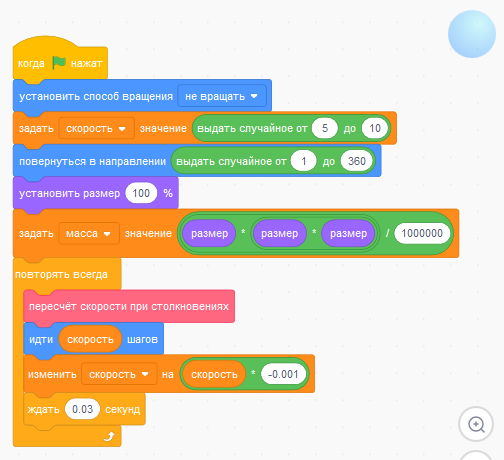
Блоки "пересчёт скорости при столкновениях" и "проверка столкновений с границами":
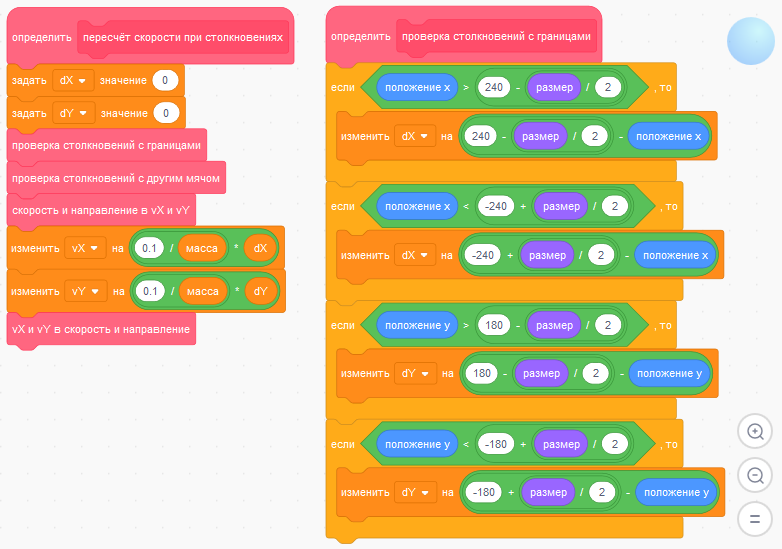
Блоки "скорость и направление в vX и vY" и " vX и vY в скорость и направление":
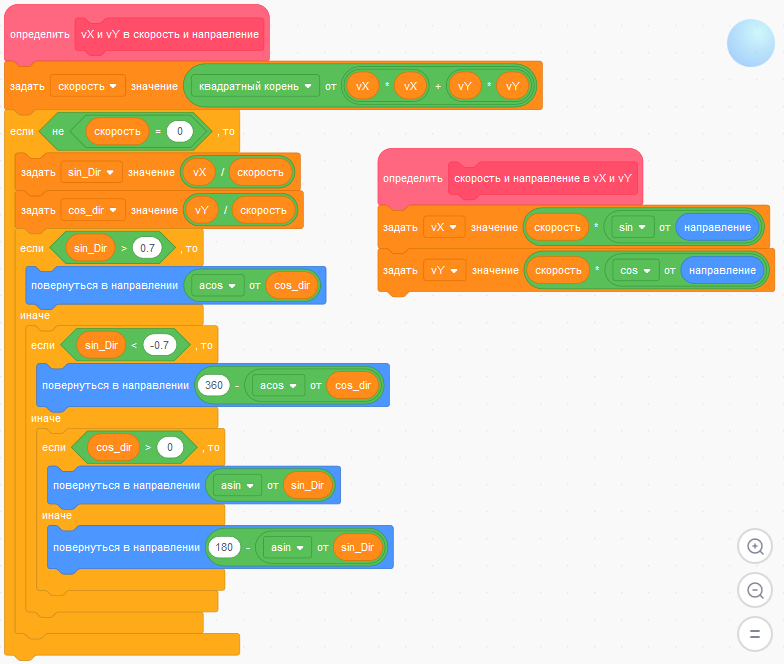
Блок "проверка столкновений с другим мячом":
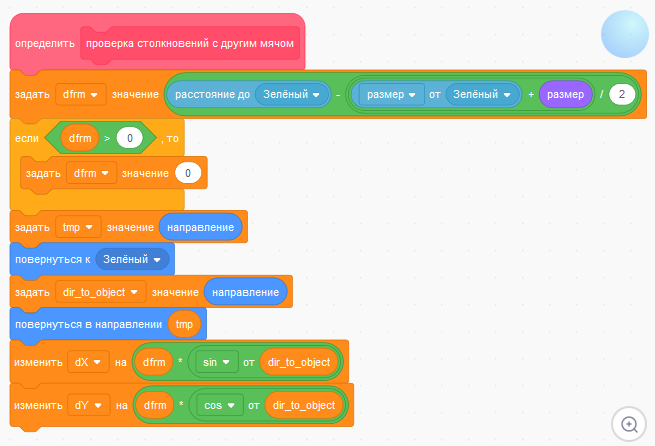
После сборки всех скриптов и проверки корректности их работы следует сдублировать их в спрайт "Зелёный". Для этого надо "зацепить" каждый скрипт мышкой и "бросить" его на иконку спрайта "Зелёный" (в этот момент она начнёт покачиваться).
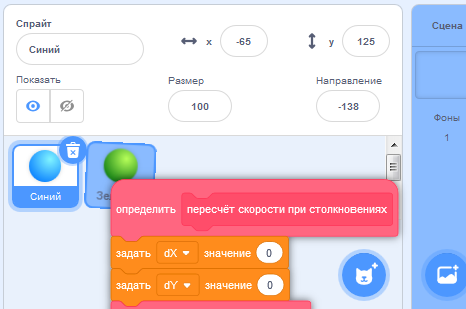
Сдублируйте все скрипты в спрайт "Зелёный". Затем выберите его, щёлкните правой кнопкой мыши по свободному месту поля скриптов и дайте команду "Очистить блоки". "Очистить" в данном случае означает "разместить в столбик".
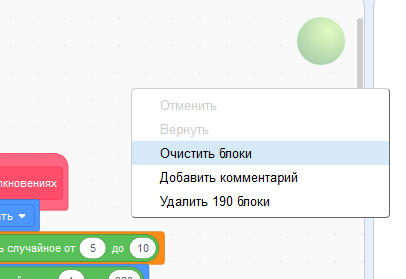
Внимательно проверьте, что удалось сдублировать все скрипты и нет лишних дублей.
Осталось поправить блок "проверка столкновений с другим мячом", заменить везде "Зелёный" на "Синий". Будьте внимательны, при этой процедуре зачастую меняется и название блока "размер от ( )" (например, на "положение X от ( )"). Блок "проверка столкновений с другим мячом" спрайта "Зелёный" должен выглядеть в итоге так.
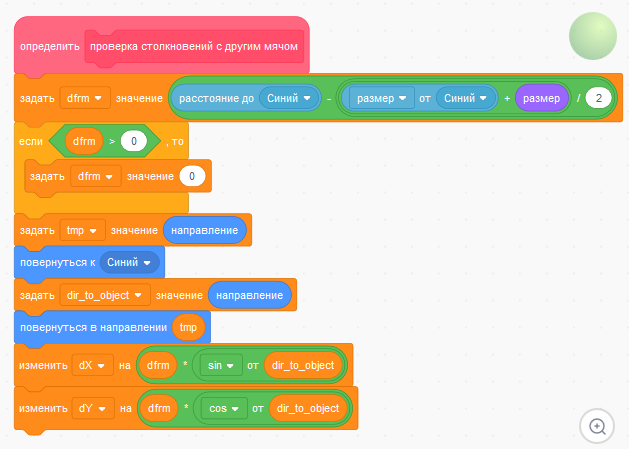
Можно также несколько поменять размер одного из мячей или обоих. Запустите программу. Движение мячей по сцене должно выглядеть примерно так:
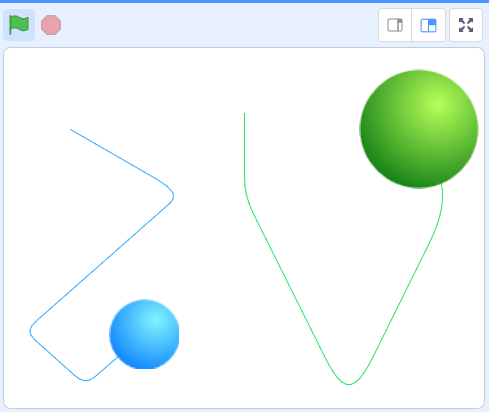
В заключение необходимо отметить, что мы никак специально не следим за соблюдением закона сохранения импульса двух движущихся тел после столкновения. Напротив, он "сам собой" естественным образом вытекает из логики работы программы.
Файл с готовым проектом: этап5.sb3
Мы приобрели представление о компьютерном моделировании движения и физического взаимодействия объектов, пора браться за решение частных проектных задач, в которых подобные модели могут использоваться.


