За последние полгода учителями найдено, изучено огромное количество сервисов и инструментов. Но меняют ли они что-то в деятельности ученика и учителя?  Стоит ли педагогический эффект  времени, затраченного на подготовку?  Можно ли их использовать для проведения экспериментов?  Спорить и сравнивать можно бесконечно, но стоит ли…

Эксперимент - метод исследования некоторого явления в управляемых наблюдателем условиях.

Возможен ли эксперимент в геометрии? Да, конечно!

Инструменты Desmos Geometry позволяют выполнять построение динамических моделей (подвижных чертежей) и “вживую” наблюдать состояние объекта при изменении начальных данных и условий, т.е. проводить эксперимент.

Один из проектов, выполненных восьмиклассниками  в Desmos Geometry, был посвящен преобразованиям многоугольников. Это были задачи на построение, но план был скорректирован для построения моделей средствами геометрических инструментов Desmos. Все построенные модели протестированы в ходе экспериментов по изменению начальных условий в ходе которых ребята  наглядно убедились в достоверности теорем.

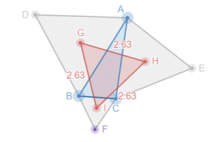
Теорема.  Если на сторонах произвольного треугольника построить правильные треугольники, то их центры образуют правильный треугольник.

 Для построения чертежа было использовано еще 18 элементов, которые были скрыты после завершения работы. Удалять их нельзя, так как они являются геометрической основой целостности полученных динамических рисунков.

Начальная фигура - синяя, конечная - красная. Эксперимент заключается в том, что при изменении синей фигуры (а ее можно перемежать за вершины) красный треугольник всегда  (при условии правильного построения!) останется правильным (равносторонним).

Теорема.  Если на сторонах произвольного четырехугольника построить квадраты, то их центры образуют другой четырехугольник, в котором диагонали равны и перпендикулярны. (24 скрытых элемента).

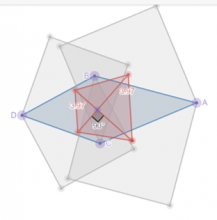
Этот чертеж переделывали дважды. Ошибочное ожидание красного  квадрата заставило заставило глубже взглянуть на признаки четырехугольников. Эксперимент  показывал, что это не квадрат! Нашли, это КВАДРАТОИД!

Главным открытием стала работа с шестиугольником. 

Построить динамический правильный шестиугольник получилось не сразу, при движении чертежа  нарушалось равенство сторон, ошибки допущенные при построении проявлялись в ходе эксперимента. 

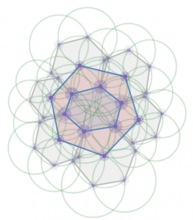
Теорема. Если на сторонах произвольного шестиугольника построить правильные шестиугольники, то шестиугольник вершины которого являются центрами этих шестиугольников правильный.

И формулировка данной теоремы оказалась неточной. Чертеж, выполненный с помощью 60 скрытых элементов, в ходе эксперимента не подтвердил утверждение: полученное преобразование оказалось неправильным шестиугольником.

Оказалось, что преобразование шестиугольников справедливо только для шестиграма - шестиугольника, у которого противолежащие стороны равны и параллельны. 

Поэкспериментировать с выполненными чертежами можно в активности.

Нужны ли подобные эксперименты в геометрии?  

 Обучающая активность (ссылка для ученика) по геометрическим инструментам.

Подробнее о Desmos в блоге Людмилы Рождественской и сообществе SIGNUM.