«Ваза в перспективе» — рисунок флорентийского художника эпохи раннего Возрождения Паоло Уччелло. Уччелло – один из создателей научной теории перспективы, приверженец пространственных построений и математически выверенных решений в живописи. Его рисунок вазы - прекрасный повод начать разговор о телах вращения, которые изучаются в школе в курсе стереометрии в 11 классе. Примеры тел вращения встречаются в архитектуре, керамике, столярном деле. В интегральном исчислении вращение тел используется для вычисления объёмов. В школьной программе рассматриваются цилиндр, конус, усечённый конус, шар. «Цилиндр» - греческое слово «kylindros», что означает «валик», «каток». «Конус» - латинское слово «conus», что означает «втулка», «сосновая шишка». «Шар» - греческое слово «сфайра», что означает мяч. Уже происхождение терминов названий тел вращения показывает целесообразность изучение темы в связи с практической деятельностью и жизненным опытом обучающихся.
Возможные подходы к раскрытию этой интересной и многоплановой темы мы обсуждали с коллегами: Ладой Анатольевной Сащенко (Санкт-Петербург) и Ириной Станиславовной Кабановой (Вологда). По большей части обсуждение велось дистанционно в гугл-документах. Постарались найти ответы на ряд вопросов. Какие примеры из окружающей жизни можно привести? Что в этих объектах могло бы заинтересовать школьников? Какие межпредметные связи можно установить? Какую проектную деятельность можно организовать? Чему можно научиться в процессе проектирования и моделирования?
Обсуждение получилось плодотворным и продуктивным, за что я чрезвычайно признательна своим творческим и профессиональным коллегам. Мы нашли множество возможностей для использования материалов по теме «Тела вращения» с позиции методики STEAM, интегрируя математику, информатику, черчение, технологию, искусство. Результаты исследования и опыт работы со школьниками были представлены нами на IX Всероссийской конференции с международным участием «Информационные технологии для Новой школы» на мастер-классе «Плоское – вращать, круглое – складывать».
Сейчас я более подробно расскажу об одном из вариантов практической работы для изучения темы «Тела вращения» с использованием 3D-моделирования в среде SketchUp. Удобно использовать бесплатную онлайн-версию SketchUp Free. Это доступный, не требующий длительного предварительного обучения редактор для 3D-моделирования. Для начала работы необходимо зарегистрироваться.
https://www.sketchup.com/ru/products/sketchup-free
Учителю достаточно показать пример моделирования тел вращения и затем предложить учащимся сделать самостоятельную практическую работу. Особенно эффективно выбирать объекты для моделирования, вызывающие эмоциональный отклик у учеников, связанные с событиями их текущей жизни. Например, после посещения гончарной мастерской мы создавали кувшины. После школьного чемпионата по шахматам - моделировали шахматные фигуры. Алгоритм моделирования состоит из четырёх шагов:
1. Создание плоскости для рисования контура.
2. Рисование контура.
3. Задание траектории вращения.
4. Вращение контура по окружности с помощью инструмента "Ведение".
Рассмотрим процесс моделирования тела вращения на примере шахматной фигуры.
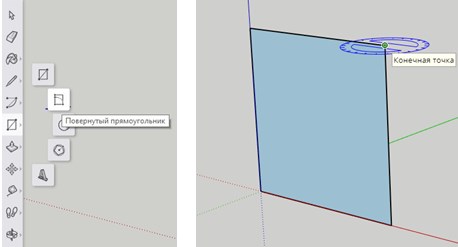
Повернутый прямоугольник.
Создадим плоскость для рисования с помощью инструмента «Повернутый прямоугольник». Начальную точку прямоугольника ставим в начало координат. Две смежные боковые стороны располагаем на красной и синей оси.
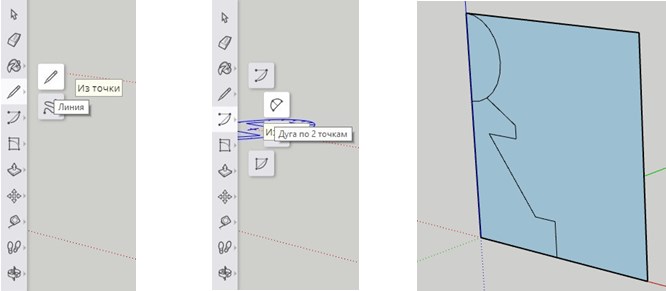
Профиль пешки.
Рисуем половину профиля пешки с помощью инструментов «Линия» и «Дуга по двум точкам». Контур должен быть замкнутой линией без разрывов.
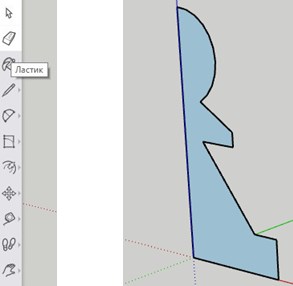
С помощью инструмента «Ластик» удаляем ненужные линии, оставляя только контур пешки.
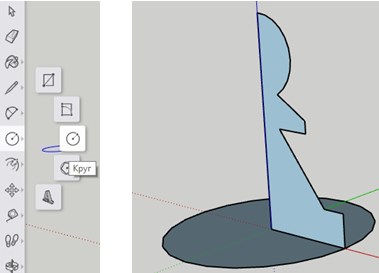
Создание объёмной пешки посредством вращения.
С помощью инструмента круг задаём траекторию вращения. Центр круга располагаем в начале координат. Выделяем границу круга с помощью инструмента «Выбрать» (стрелочка).
После выделения окружность станет синего цвета. Выбираем инструмент «Ведение» наводим его на контур пешки и щелкаем левой кнопкой мыши.
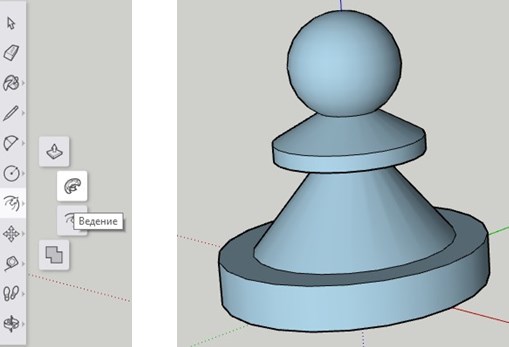
Практическая работа для изучения с использованием 3D-моделирования даёт положительные образовательные результаты при изучении темы «Тела вращения». Сконструировав собственные модели тел вращения, повертев и покрутив их, ребята получают навыки построения тел вращения, развивают пространственное воображение, лучше решают задачи на вычисления объёмов, построение сечений и комбинацию тел вращения.
О работе в SketchUp:
Моделируем в SketchUp. Инструкция «Дом»
Моделируем в SketchUp. Триумфальная арка
Моделируем в SketchUp. Тайницкая башня



