Случилось так, что в рамках школьного дистанционного проекта по Балтийскому морю нам с коллегами нужно было "поднять" морскую тематику посредством математических активностей. Опираясь на свой же довольно удачный опыт по поиску прототипов среди англоязычных публикаций, мы решили поискать с простым запросом teacher desmos sea problem в google-поиске.
STEAM-АКТИВНОСТИ И МОРСКАЯ ТЕМА
Что бывает, когда помимо "сухой математики" в активностях начинаешь интересоваться историями - историями открытий, изобретений, подвигами ученых, инженеров и испытателей.Надо сказать, что улов был удачным, но пойманную "рыбку" требовалось переработать под свои задачи - те программные темы для 6-ых - 11-ых, которые актуальны были для нас на тот момент.
Как всегда, мы начали с перевода. Кое-что из переведенного в проектные задания для учеников, правда, не вошло, но зато осталось опубликованным в сообществе (см Примеры 2 и 3 этой публикации).
Пример 1. Истории великих экспериментов
Но нам попалась и такая история, мимо которой мы просто не могли пройти. С первого взгляда бросалась в глаза ее особенность: математические задания разворачиваются в контексте сразу двух крупных событий в истории науки и техники, да еще и связанных между собой именами их участников - отца и сына Пиккаров. Старший из них сконструировал и испытал воздушный шар, на котором в 1932 году поднялся на рекордную высоту (на тот момент). А его сын Жак в составе команды из 2-ух участников первым в истории человечества в 1960 году на батискафе Триест опустился на рекордную глубину и посетил Челленджерскую бездну Марианской впадины. Такие истории, как нам казалось, не могли не вдохновить наших учеников-подростков.

Из оригинала у нас получились сразу две адаптации - для 7-го и для 6-го класса - в обеих делаются разные акценты на разных темах математики, но с сохранением оригинальной истории.
Их отличительной чертой является сравнительно большая (чем в других математических заданиях) порция текстов на функциональное чтение (понимание и интерпретацию) информации.
Исследование морских глубин и воздушных океанов (линейная зависимость, 7 класс)
Исследование морских глубин и воздушных океанов. Адаптация для 6 класса (числовая прямая)
Хочу вытащить на поверхность из последней активности удивительный сайт https://neal.fun/deep-sea/, который нашла в процессе переработки оригинала в задание для 6 класса и смогла, как мне кажется, удачно его использовать для составления инструкции на 7-м слайде.

Вот немного скриншотов и ответов учеников в процессе выполнения активностей:
Что удивило?
- Удивило: Одно летит , другое плавает
- Удивило: то что даже тогда люди делали такие успехи
-
Удивило: что получилось сделать батискаф, который смог выдержать сильное давление на глубине, и который смог погрузиться на такую большую глубину (на основе модели шара летящего наверх).
-
Что в одной семье такие талантливые люди, отец покоряет высоты, а сын - глубины.Что в такое время люди совершали подобные эксперименты
Что заметили?
- я так думаю, потому что на него давила гравитация(то есть ускоряла)
- Я заметила: чем глубже спускается батискаф,тем меньше времени он затрачивает
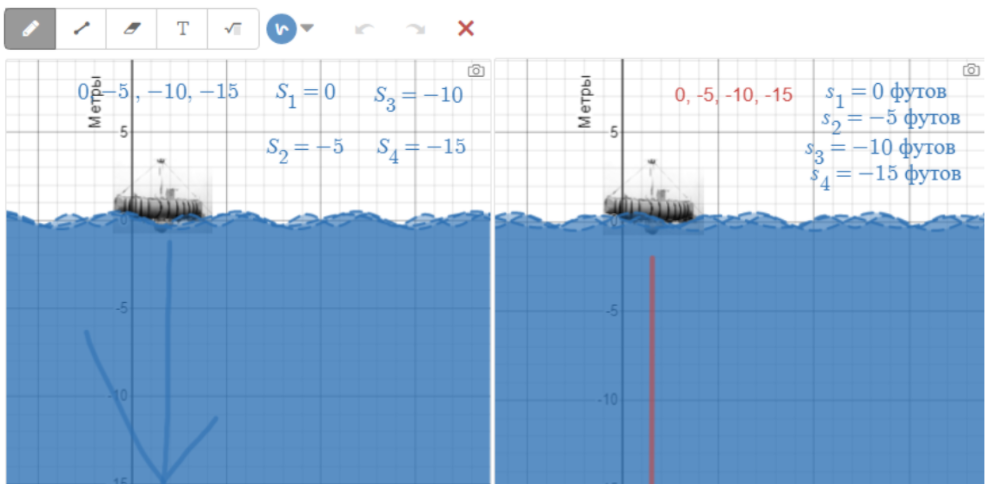
- Я заметил: Если положительное , то плывёт в верх , если отрицательное, то вниз
Учителю есть что обсудить с учениками, глядя на эти их рисунки:
Примеры 2 и 3. ЗАДАНИЯ, ОСНОВАННЫЕ НА ПРОБЛЕМАХ И НА ДАННЫХ НАУЧНЫХ НАБЛЮДЕНИЙ
Это тема, которая, правда, уже здесь поднималась. Но ее опять хочется "проветрить", пусть она и не находит пока особого отклика. ![]()
Заметила, что коллеги больше откликаются на публикации "новой" (но, на самом деле, десятой по счету) активности про какую-нибудь линейную функцию. Такую, каких было уже много. Добротную, да, с многочисленными заходами разнообразных упражнений на угловой коэффициент и проверку принадлежность точки данной прямой и т.д. и т.п. И совершенно типовую, просто кальку с учебника...
Понятно, что с учениками "нужно отрабатывать навыки" и вообще "проходить темы".
Но, мне кажется, в рабочей текучке мы не успеваем ставить этот важный вопрос: а зачем?
Зачем нужна эта самая линейная функция? Или показательная? Где они в реальной жизни встречается то? И какую из них правильнее взять для описания сложной модели глобального процесса, происходящего на наших глазах? Такого, например, как подъем уровня мирового океана.
Вопросы эти, вроде, простые и примеров применения этих и других функций, у вас, наверняка, много, но, уверена, такого вы еще не видели...
2. ИНСТРУМЕНТ ПРОГНОЗИРОВАНИЯ ПОВЫШЕНИЯ УРОВНЯ МОРЯ...

В этой активности Повышение уровня моря использован интересный симулятор, который с помощью ползунка помогает увидеть, какие территории окажутся под водой при каждом подъеме уровня моря на несколько футов. Жаль, симулятор только для Америки. Пример.
3. Индикаторы изменения климата
Активность Индикаторы изменения климата
Учащиеся используют понятие корреляции и регрессии, чтобы делать прогнозы об окружающей среде в 2100 году.
В этой активности используются только данные индикаторов изменения климата (по EPA).
Основные индикаторы изменения климата
- Содержание тепла в океане
- Концентрации двуокиси углерода в атмосфере
- Глобальный средний уровень моря
- Изменение протяженности или массы криосферы

В моей публикации на фб задала вопрос, а нужны ли вообще подобные активности? Может, и время на их перевод и адаптацию тратить не стоит?
Часть коллег отозвалась размышлением, например, Светлана Романова прокомментировала так:
...нет в нашей постсоветской учительской культуре годами наработанной привычки смотреть дальше страниц учебника. И работать проектами многие только начинают учиться. И чем больше будет таких примеров, от которых фантазия учителя сможет оттолкнуться, тем быстрее наще образование начнет выходить на другой уровень
А что по этому поводу думают читатели Новатора?
Статьи по теме
- Как совершенствовать навыки групповой работы во время пандемии
- Как на математическом языке говорить с учениками о пандемии, вакцине и вакцинации? Примеры активностей
- Общешкольный проект "Карантин - необитаемый остров"
- День Дистанта в школе
- Побег из классной комнаты: День дистанта
- Побег из классной комнаты. Изменение оргформ
- Что же отличает задания нового типа? Появится ли дигитальная дидактика?
- Алиса в стране чудес. Деликатесы дидактики
- STEAM в начальной школе: новая жизнь идей из интернета
- Постер как форма упаковки информации в STREAM-проекте: Колдер и Вазарели
- Идеи в духе STEAM: геометрический конструктор на основе рисунков Google
- БРИКОЛАЖ как образовательный тренд
- В начале была цифра?
- Дни математики, программирования и робототехники в школе: первый опыт
- STEAM в начальной школе: геометрия комнаты
- О математических иллюстрациях к художественным произведениям
- Мейкерство с бумагой и цифрой: зоетроп (движущиеся картинки)
- Мейкерство с бумагой и цифрой: фенакистископ
- Мейкерство с бумагой и цифрой: тауматроп
- Кодируй, как пират!
- Программирование для воссоздания картин: математика и искусство вместе
- В начале была цифра?
- Искусство создания снежинки, или Как скоротать зиму...