Введение. Откуда опять тут растут кубики.

«Кубичная» тема поднималась мною еще на Галактике Интел: хотелось привлечь внимание к незаслуженно забытым, а для многих незнакомым кубикам Никитиных, показать их возможности, потенциал и актуальность для разных возрастов и учебных ситуаций. Позже на Новаторе появился материал о моделировании псевдообъемных кубиков и конструкций из них в Paint.

Приятно было увидеть, что тема востребована и интересует многих, находит развитие в поиске иных форм и инструментов для работы, становится сырьем для большого количества разных заданий. Компьютерные симуляторы, при помощи которых можно моделировать конструкции из кубиков, наборы заданий для них, место таких заданий в школьном курсе математики были рассмотрены в публикациях Людмилы Рождественской на Новаторе, а еще раньше - на Галактике.

Прекрасные программы и упражнения, разработанные для зарубежных педагогов, а поэтому, как правило, англоязычные, не остановили группу энтузиастов, и появились инструкции и переводы упражнений на русский язык.
 А лето еще не закончилось, можно найти еще время и поиграть, и включить примеры заданий в рабочую программу по предмету.

Почему реальные кубики?

Не стоит отвергать  вещные, манипулятивные практики, работу учащихся с реальными объектами. В начальной школе никогда не бывает мало игры с настоящими товарищами и настоящими предметами, которые можно крутить, перекладывать, комбинировать, исследовать возможности и свойства в натуре. Для учащихся постарше, особенно испытывающими затруднения в аналитике, со слабо развитыми пространственными представлениями и отставанием в формировании логических операций виртуальные модели могут быть сложны, а мысленные преобразования недостижимы. Материальные кубики могут быть хорошим подспорьем, инструментом самопроверки, объектом для многократных подходов к всестороннему исследованию. К тому же в современных школах незаслуженно задвигается на задний план геометрия. Нынешние дети, выросшие в мире гаджетов с плоской картинкой, в средах реалистичных игр, где не надо представлять «изнанку» или «тыл» предметов, а достаточно легким движением изменить ракурс, и все откроется, испытывают трудности с целостным представлением объектов.

На уроках геометрии таким ученикам сложно представить, как выполнить то или иное построение, и что получится, если это построение будет выполнено. На уроках технологии (черчения) возникают сложности с моделированием, ошибки в разметке. Задачи по вычислению объемов тел и площадей фигур вызывают затруднения, потому что представления об объекте ошибочны или их нет. Использование вербальных описаний совокупности фигур без сопровождающего изображения вызывают трудности в изображении. А умение оперировать разными сигнальными системами, переводить информацию из одного вида в другой — одно из важнейших как в обыденной жизни, так и во многих профессиональных сферах.
Считаю, что наборы самых разных кубиков должны в достаточном количестве быть в каждой школе и быть доступными для всех учеников с 1 по 11 (12) класс, и это не исключает возможности использовать компьютерные инструменты и модели. Разумное сочетание тех и других будет только на пользу.

Где ж их на всех понабраться?

Если нет финансовой возможности приобрести кубики в необходимом количестве, а спонсорская помощь по каким-то причинам эту проблему не решает, остается делать самим.
Изготовление наборов кубиков из разных материалов — сам по себе увлекательный проект. Здесь много творчества (а из чего и как можно сделать), переходящего в технологию: деревянные, фанерные, картонные, пенопластовые (пенопласт остается как упаковочный материал при покупке техники), пенополистирольные (прекрасный материал, отлично пилится канцелярским ножом), бумажные (оригами).

Схем складывания кубиков оригами несколько, и есть много тематических сайтов, где размещены подробные инструкции. Для пущей мотивации я иногда выбираю те источники, где продукт показан наиболее ярко и впечатляюще, например, инструкция к кубикам больше приглянулась на сайте Самоделки. Но вначале неплохо бы спросить у чеников - может, кто-то из них уже умеет делать кубики из бумаги и может научить товарищей?

Отдельная задача - как добавить окраску: брать уже окрашенный материал, или расцвечивать его при помощи красок? Какие краски можно использовать, что доступно по цене, допустимо для этого материала, разрешено к использованию в детских учреждениях? Насколько легко наносить краску, сколько будет высыхать, можно ли использовать самоклеящуюся пленку?  Так в процессе создания простых игрушек школьники ищут ответы на совсем неигрушечные практические вопросы и обучаются полезным навыкам.
Немало математики, геометрии, черчения: построение разверток, разметка на материале, расчет количества требуемого материала. Изучение уже имеющихся примеров наборов кубиков (на сайтах производителей, на сайте Никитиных), придумывание собственных. Взаимодействие с непедагогическим персоналом школы (рабочим по обслуживанию здания, завхозом) и сторонними организациями (договоренности о материале — отходах производства, или субботник в обмен на материалы, или обработка материалов промышленным способом). Опрос семей на предмет пожертвования для школьных нужд разукомплектованных или «переросших» своих маленьких хозяев кубиков (например, кубики с картинками), переделка их для школьных нужд. После изготовления — обучение младших товарищей играм и упражнениям с кубиками.

И ради чего это все затевается?

Кроме уже рассмотренных в вышеприведенных публикациях заданий на пространственное восприятие — интересных и полезных, использование кубиков как дидактических пособий при изучении тем «Квадрат. Прямоугольник. Площадь» и «Куб. Прямоугольный параллелепипед. Объем».
Один из самых методически мощных наборов, на мой взгляд — игра «Сложи узор» от Никитиных http://nikitiny.ru/slozhi-usor
С этим набором можно «расти» долго, в процессе манипуляций изучая множество свойств объектов и овладевая различными мыслительными операциями.
С малышами — изучение цвета, счет, понятия больше-меньше, ближе-дальше.

Чуть старше — построение узора по образцу, придумывание своего узора, построение узора по словесному описанию. Изучение простейших свойств: равенство фигур, подобие, параллельность, прямоугольность. Эмпирическое овладение понятиями «квадрат», «куб», «вершина», «ребро», «грань». Вариативность подсчета (сосчитать количество кубиков в конструкции разными способами). Коммутативность сложения. Умножение. Измерение линейных размеров и углов.
Понятие существенных и несущественных признаков. Анализ условий разных задач для выделения существенных и несущественных признаков.
Еще старше:
Понятие площади как меры для места, занятого видимой плоской фигурой или для закрашенной части 

плоскости. Равенство площадей у равных фигур. Перекомбинация элементов для удобного вычисления площади, понятие равновеликих фигур. Площадь сложной (большой) фигуры как сумма площадей компонентов. Площадь прямоугольного треугольника. Площадь полной поверхности тела. Коммутативность умножения. Развертки кубиков с разной окраской.

Понятие объема как меры места, занятого телом в пространстве или количества материала, требуемого для изготовления. Равенство объемов у разных тел. Тела равные и подобные. Объем параллелепипеда, вычисление разными способами. Построение сложных тел по образцу. Построение тел по описанию. Придумывание своих конфигураций, загадывание товарищам по словесному описанию. Виды.

Проекции точки, линии, фигуры, тела. Представление сложных тел как совокупности элементов. Площадь поверхности сложного тела. Площадь поверхности тела с частичной раскраской элементов. Вычислительные «лайфхаки», основанные на перекомбинации. Построение сложных конструкций со сквозным или несквозным отверстием, вычисление объемов и площадей.

Вычисление длин ломаных, которые суть границы между разноцветными раскрасками. Вычисление площадей фигур, получившихся мысленным пересечением данных сложных. Вычисление площадей фигур (общих границ), получившихся объединением сложных фигур по граням. Вычисление объемов тел, получившихся при мысленном пересечении данных сложных. Построение разверток некоторых сложных тел.
Масштаб.

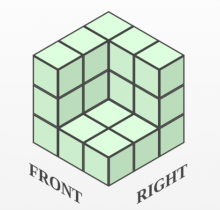Дополнительно:

Опыты для эмпирического введения понятия «плотность». Выполнение необходимых замеров, поиск информации, вычисления, проверка гипотезы.

Рычаги, равновесие
Построение чертежа в двух, трех видах.
Построение сложносоставленных фигур (тел) в графических редакторах и САПР

Программирование построения простых и сложных фигур (тел) в разных средах

3D моделирование виртуальное и материальное

Понятие перспективы

Варианты кубиков:
Кубики для рассказывания историй (конечно, картинки уже другие)

Кубики Блума

Кубики — игральные кости

Все, что «мета...»: развитие регулятивных навыков, целеполагание, разбиение задачи на подзадачи, коммуникативные навыки, развитие речи, овладение научным языком, развитие самостоятельности, формирование умений поиска и обработки информации, развитие внимания, аккуратности, творческих способностей, технологических навыков, дальнейшее «прокачивание» изобразительных навыков…

И напоследок

Даже солидные одиннадцатиклассники и одиннадцатиклассницы, старающиеся изо всех сил казаться взрослыми и умудренными, с большим удовольствием играют и в виртуальные, и в реальные кубики, выполняя бесхитростные упражнения. И вспоминают при этом беззаботное детство, собственные кубики, связанные с ними события и людей. Бывает, у них некоторые задания никитинского «Сложи узор» вызывают затруднения. А иногда эти великовозрастные детинушки, вращая в руках детали или рассматривая какую-то конструкцию со всех сторон, делают личные мини-открытия. И очень хочется эти мгновения возвращения в детство задержать, продлить, зафиксировать, зная, что в дальнейшем этих ребят ждут непростые ситуации и времена. А возможности снова окунуться в детские годы может и не быть.

Так что давайте все же не забывать кубики