Обучение, основанное на артефактах – инновационный подход школьного преподавания.
Реализация данной модели обучения является достаточно сложной, но очень актуальной в условиях современной школы, так как при работе с артефактом процесс освоения новых знаний направлен на активное, творческое познание.
Возникла идея создания междисциплинарного образовательного курса для учащихся шестых классов, основанного на артефактах средневековья древних городищ бассейна реки Чепцы. Курс включает в себя три предметные области: математика, история, проектная деятельность. За основу берутся артефакты средневековья, далее ставятся учебные задачи, происходит проектирование учебных ситуаций. Анализ артефактов происходит со стороны двух предметных областей математики и истории, а на уроках проектной деятельности учащиеся выполняют изделия - копии артефактов.
Форматом проведения являются уроки и творческие мастерские. На одну учебную неделю берется определенный артефакт. На уроках истории за основу взят учебник Ивановой М.Г. История Удмуртии 6 кл. Проектные продукты выполняются на занятиях по проектной деятельности.

Анонс проекта.
Город Глазов на реке Чепце зародился в XVI веке как деревня. В эпоху средневековья в бассейне р.Чепцы проживали предки современных удмуртов. Уже более ста лет археологи ведут исследования этой территории. За это время при раскопках найдены уникальные предметы.

Мною представлена дидактическая разработка части курса по математике.
Артефакт Пряслице
- Артефакт: Пряслице
- Тема: Урок 1-2. Решение практико-ориентированных задач на нахождение площади круга и объемов пространственных фигур.Урок 3. Построение геометрических объектов с помощью динамической математической среды Geogebra
- Предметные результаты:
Наглядная геометрия
Учащийся научится:
• использовать геометрический язык для описания предметов окружающего мира; разовьёт пространственное представление, изобразительные умения и навыки геометрических построений;
• оперировать понятиями: фигура, точка, отрезок, окружность и круг;
• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры и их элементы;
• изображать изучаемые фигуры от руки и с помощью линейки и циркуля; выполнять измерения длин, расстояний с помощью инструментов для измерений длин;
• определять по линейным размерам развёртки фигуры, линейные размеры самой фигуры и наоборот.
Учащийся получит возможность:
• научиться вычислять объём пространственных геометрических фигур;
• углубить и развить представления о пространственных геометрических фигурах.
- Предметное содержание:
Наглядная геометрия
Геометрические фигуры
Фигуры в окружающем мире. Наглядные представления о фигурах на плоскости: окружность, круг. Изображение основных геометрических фигур. Понятие площади фигуры; единицы измерения площади. Наглядные представления о пространственных фигурах: шар, цилиндр. Изображение пространственных фигур. Примеры сечений.
Понятие объема; единицы объема.
Решение практических задач с применением простейших свойств фигур.
Числовые и буквенные выражения. Уравнения.
Формулы.
Геометрические фигуры. Измерения геометрических величин.
Окружность и круг. Длина окружности.
Наглядные представления о пространственных фигурах: цилиндр, конус, шар, сфера.
- Используемые инструменты и ресурсы: мобильный компьютерный класс, динамическая математическая среда Geogebra.
- Тип учебной ситуации: ситуация-проблема.
- Учебная задача: нахождение площадей с использованием формулы площади круга, нахождение объемов с использованием формул объема цилиндра, шарового сегмента для решения практических задач, требующих проведения небольших исследований, решение задач на построение в Geogebra.
- Описание учебной ситуации:
Рассмотрите артефакт-картинку.

Раскопки 1999 г. Рис.1
Учащимся для работы на уроке раздать карточку с рисунками пряслиц в масштабе 1:1. Провести небольшую беседу с учащимися о пряслицах.

Раскопки 1999 г. Рис.2
|
Задания
|
Ответы и решения |
Комментарии и дополнения |
|
Определите размеры пряслиц на рисунке 1 и на рисунке 2 |
Пряслице на рисунке 1 в основании имеет R=1,25 см, r=0,5 см. Высота цилиндра равна 1 см. Пряслице на рисунке 2 в основании имеет R=2,15 см, r=0,5 см. Высота шарового сегмента равна 0,6 см. |
Обсудить с учащимися, какие размеры дают характеристики пряслиц. Учащиеся должны выполнить соответствующие измерения на предложенных изображениях пряслиц. Объяснить, что важной характеристикой шарового сегмента является его высота. |
|
Определите форму пряслиц на рисунке 1 и на рисунке 2 |
Пряслице на рисунке 1 имеет цилиндрическую форму, пряслице на рисунке 2 имеет линзовидную форму. |
Были найдены пряслица шаровидной, конической формы. Что такое линзовидная форма? Это форма, которая получается при совмещении двух шаровых сегментов. Объяснить учащимся, что шаровой сегмент – часть шара, отсекаемая от него плоскостью.
|
|
Рассчитайте площадь основания пряслиц на рисунке 1 и рисунке 2, приняв π
|
Формула площади круга S= S1= S2= |
|
Рассчитайте объемы пряслиц на рисунке 1 и рисунке 2, приняв π≈3. Можно ли утверждать, что площадь основания первого пряслица и его объем равны? |
Формула объема цилиндра V= V1=
V2=2∙ Утверждать, что площадь основания первого пряслица и его объем равны нельзя, так как площадь и объем имеют разные единицы измерения. |
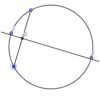
Учитель представляет учащимся две незнакомые формулы для нахождения объемов. Формула нахождения объема цилиндра V= Формула нахождения объема шарового сегмента V=πh2(RШ-h/3), где h-высота сегмента, RШ-радиус шара для второго пряслица. Возникает проблема в определении радиуса шара для второго пряслица. Для решения этого вопроса учащимся предлагается на карточке зафиксировать три точки, которые лежат на окружности большого круга шара, построить эту окружность, а затем приблизительно определить радиус шара RШ
Следующая проблема второго пряслица возникает с отверстием. Ее можно решить, условно приняв форму отверстия за цилиндр с высотой 1,2 см и радиусом основания 0,5 см. |
|
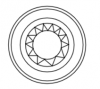
С помощью динамической математической среды постройте изображение пряслица рисунка2.
|
При работе в Geogebra требуется построить конические окружности R1=2,15 см, R2=2 см, R3=1,5 см, R4=1,2 см, R5=0,8 см, R6=0,5 см. Затем частично нанести узор. |
|
8. Оценивание.
Результаты заданий 2-5 заносятся в таблицы и сдаются на проверку учителю. Результаты задания 6 скидываются в общую папку на компьютере для дальнейшего совместного обсуждения результатов работ и качественной оценке результата учителем.