Я хотела бы рассказать о проектно-исследовательской работе, посвящённой моделированию и исследованию свойств трёхмерных фракталов. Тема была предложена старшеклассникам для подготовки к научно-практической конференции. Важная педагогическая задача работы над проектом заключалась в изучении содержательных примеров использования математических идей и методов в различных областях окружающего мира.
К сожалению, фрактальная геометрия не входит в базовый курс школьной математики, хотя фрактальные конструкции гораздо лучше обеспечивают представление многих природных явлений, чем объекты классической евклидовой геометрии.
Почему геометрию называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. Облака – это не сферы, горы – это не конусы, линия берега – это не окружности, и кора не является гладкой, и молния распространяется по прямой… Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно.
Бенуа Мандельброт
Работа над проектом началась со знакомства с базовыми понятиями теории фракталов.
Фрактал (от латинского fractus, означающего «сломанный, разбитый») — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
В общем случае, термин «фрактал» может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
- самоподобие (иерархический принцип организации);
- нерегулярность (принцип неопределенности границ);
- способность к саморазвитию (принцип непрерывности формообразования);
- дробная метрическая размерность.
Основоположник теории фракталов Бенуа Мандельброт предпочитал визуальное представление математических задач символьному. Мандельброт связал фрактальную геометрию с географией, биологией, физикой. В современном мире фрактальную графику применяют в создании текстур и фонов в фантастических фильмах и компьютерных играх. Мандельброт отмечал и эстетическую красоту фракталов.
Может ли чистая геометрия «человеку с улицы» показаться прекрасной? Точнее, может ли фигура, описываемая простым уравнением или правилом построения, быть воспринята человеком, не связанным с геометрией, как фигура, имеющая эстетическое значение, а именно, быть декоративной, а возможно и видом искусства? Если эта геометрическая фигура - фрактал, то ответ - да.
Бенуа Мандельброт
Практической частью работы стало 3D-моделирование и изучение свойств трёхмерного фрактала губка Менгера.
Губка Менгера — геометрический фрактал, трёхмерный аналог ковра Серпинского.
Фрактал ковер Серпинского получается путём вырезания частей из квадрата. Возьмём квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. Ковёр Серпинского имеет нулевую площадь.

Алгоритм построения губки Менгера происходит по тому же принципу, что и ковёр Серпинского. Строится губка Менгера на основе куба. Каждая грань куба, имеющая единичную длину, делится на 9 равных квадратиков так же, как и при построении квадратного ковра Серпинского. В результате исходный куб разбивается на 27 одинаковых кубиков с длиной ребра, равной 1/3. Затем, удаляя 7 кубиков (один центральный и 6 из центра каждой из граней), противоположные грани исходного куба соединяются сквозным центральным отверстием квадратной формы. В результате из 27 остается 20 маленьких кубиков. Такая итерационная процедура с вырезанием сквозных отверстий и последующего превращения каждого оставшегося кубика в 20 еще более мелких (размера в три раза меньше исходного) продолжается до бесконечности. В результате этих операций образуется самоподобный объект, называемый губкой Менгера. Губка Менгера имеет нулевой объём, но бесконечную площадь граней.
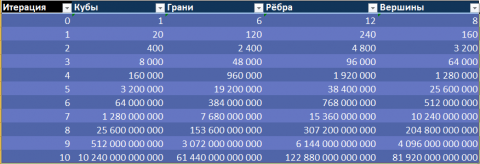
Количество кубов увеличивается на каждом шаге в 20 раз. Соответственно, в 20 раз увеличивается и количество граней, рёбер, вершин. Рост количества элементов происходит в геометрической прогрессии, следовательно для 3D-моделирования потребуется мощный и производительный компьютер. Ресурсов моего ноутбука хватило на четыре итерации.
Казалось бы, фрактальные конструкции являются объектами чистой математики. Но они нашли своё материальное воплощение в архитектуре. Архитектура, начиная с фрагментов, деталей и заканчивая пространством города в целом – это система, обладающая фрактальными свойствами.

Сначала пористость была планировочной идеей, — рассказывает Холл, — как возможность связать здание с ландшафтом. Затем она стала конструктивной идеей — как сохранить конструкцию здания, вынимая из него куски железобетона. И наконец, она стала социальной идеей — эти вырванные куски, эти ниши в здании стали пространством общения для студентов, архитектура стала катализатором социального пространства.
Источник: «Феноменологический подход к архитектуре»
Приведу пример построения губки Менгера в Blender.
Blender - свободный кросплатформенный редактор трёхмерной графики с открытым кодом. Редактор обладает широчайшими возможностями для трёхмерного моделирования, анимации, визуализации, работы с физикой, рендеринга и постпродакшна. Ранее на портале сообщества «Образовательная галактика Intel» публиковала материалы об этом профессиональном редакторе 3D-графики.
Открываем Blender. Удаляем камеру и источник освещения. Оставляем только куб.
Переключаемся в ортогональную проекцию.
С помощью копирования кубиков создаём создаём заготовку для первой итерации губки Менгера.
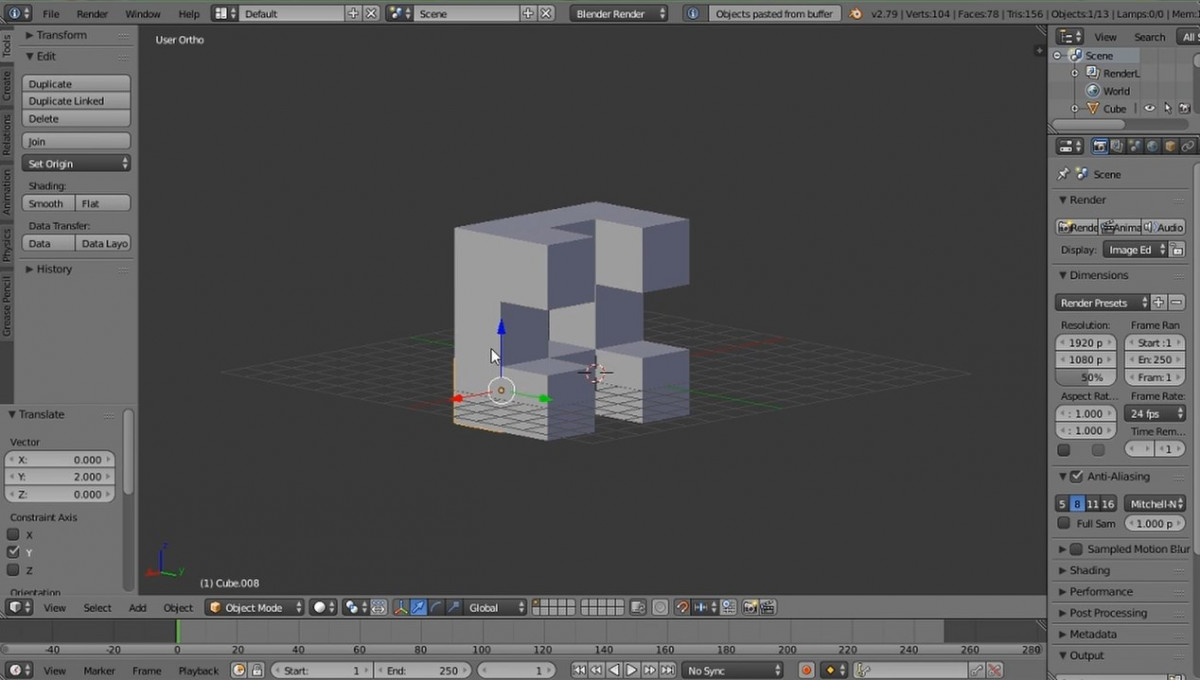
Объединяем кубы (сочетание клавиш Ctrl+J).
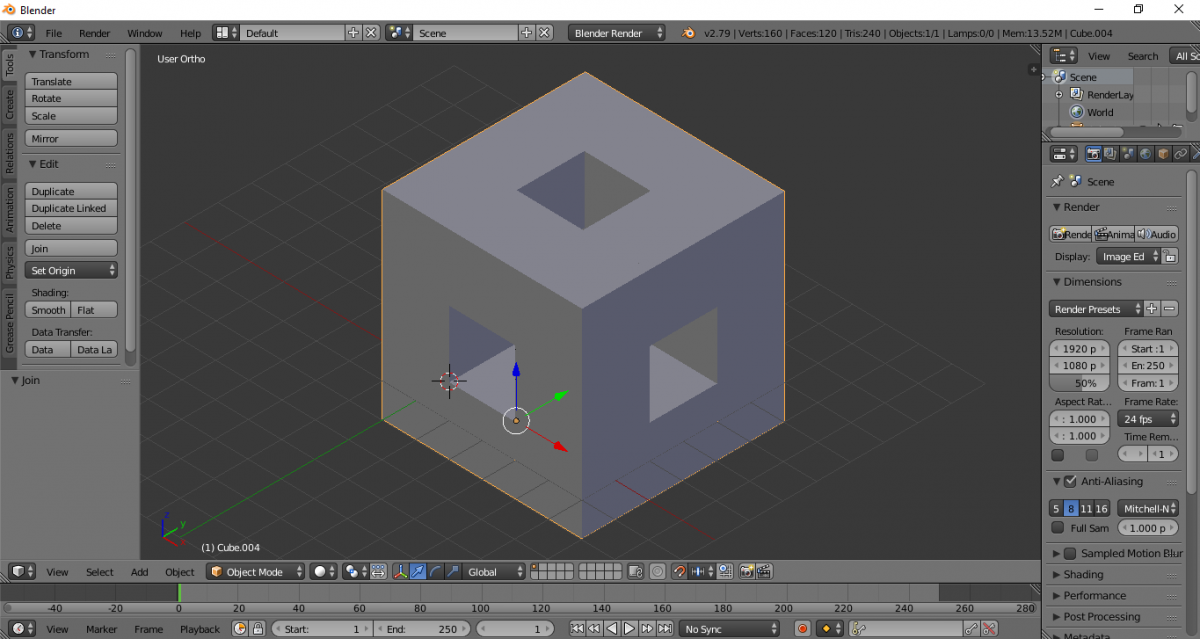
Переключаемся в ортодоксальную проекцию. Выделяем грани. В виде спереди, сбоку и сверху и скрываем их (клавиша H).
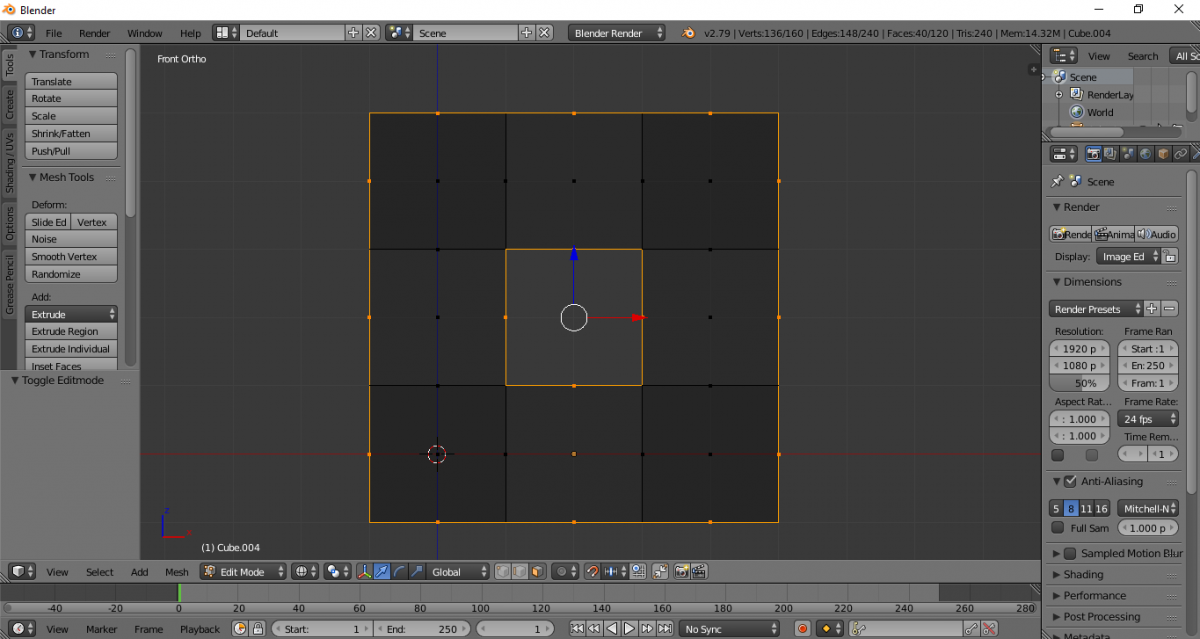
Получившуюся фигуру удаляем.
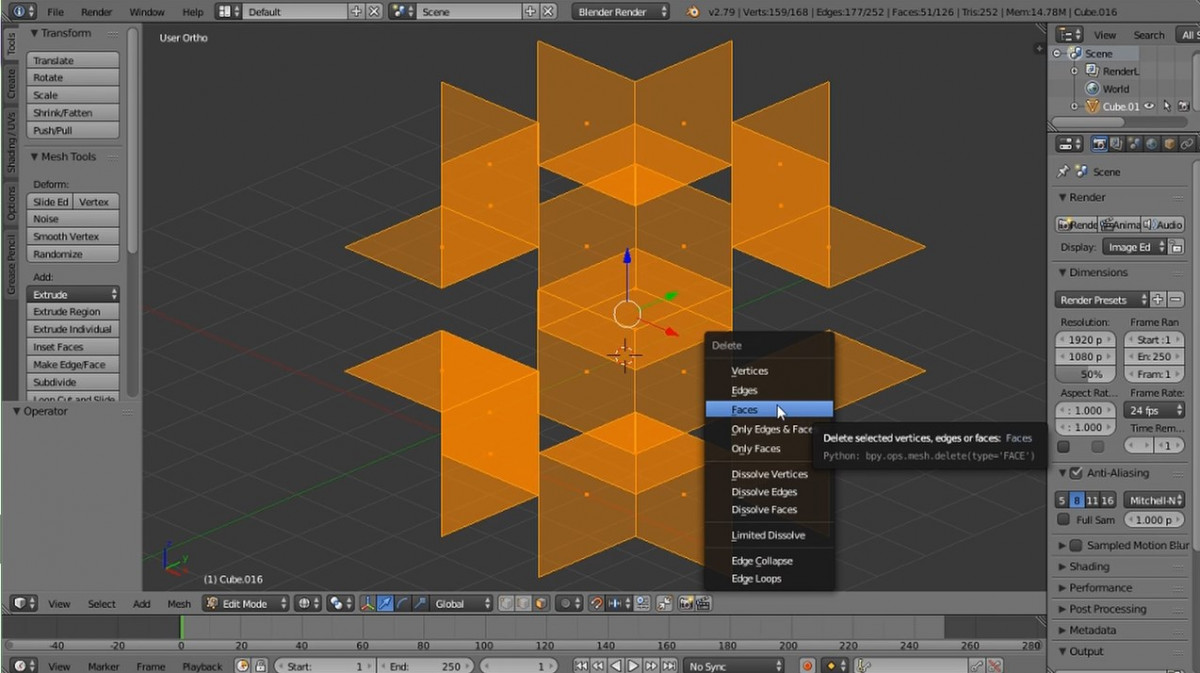
Возвращаем фигуру (сочетание клавиш Alt+H) и удаляем дубликаты. После создаем следующую фигуру, по аналогии с предыдущим шагом.
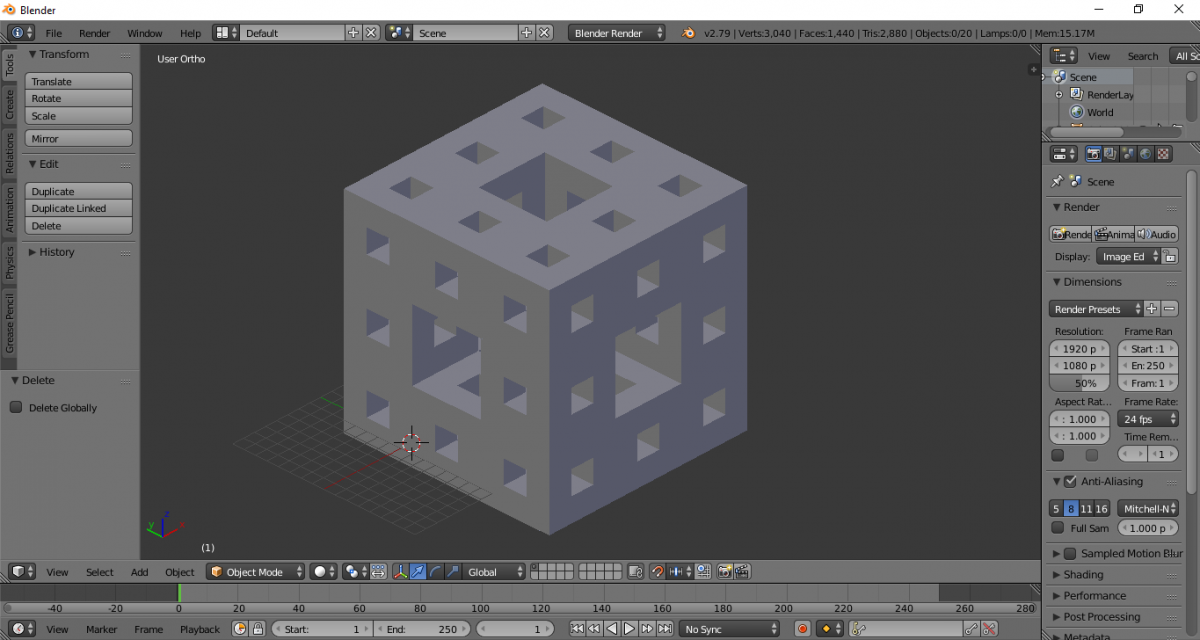
Повторяем итерацию ещё раз. Выделяем необходимые элементы.
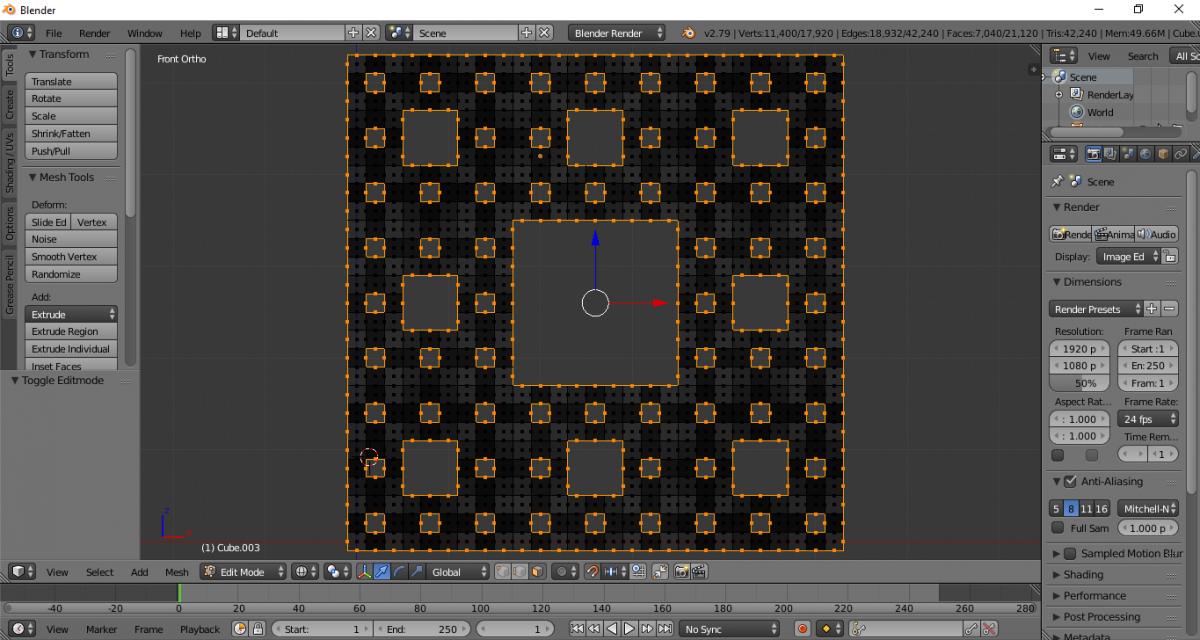
Удаляем лишние грани.
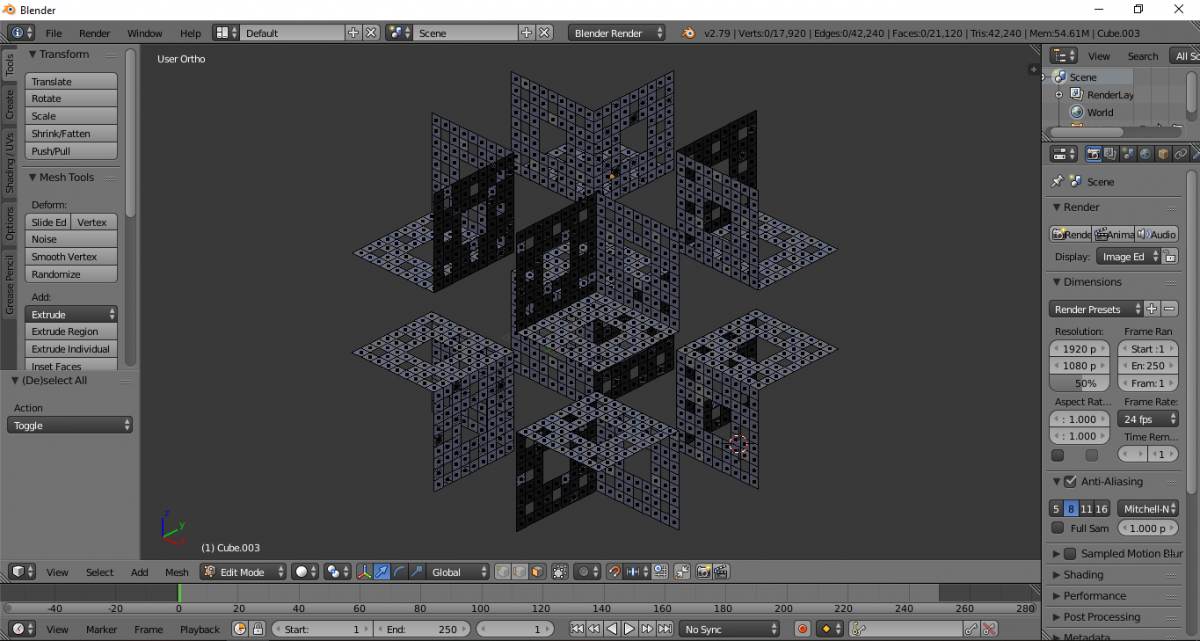
Трёхмерный фрактал губка Менгера построен.
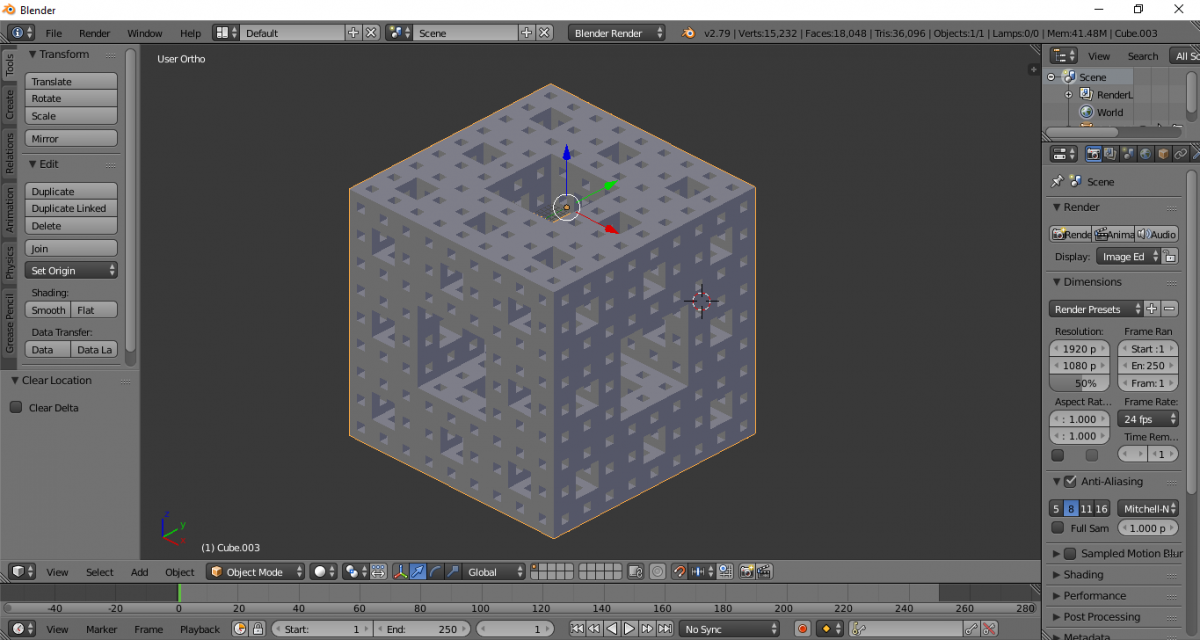
Отмечу, что привела лишь один из возможных способов моделирования губки Менгера. Поиск других, возможно, более оптимальных способов построения, является задачей проектно-исследовательской работы. Что меня особенно порадовало и даже несколько приятно удивило, так это то, что тема вызвала интерес у учеников. Они предложили содержательные идеи для развития и доработки проекта.




