Как превратить привычку учеников набирать текстовые сообщения на телефонах в математическую задачу? Причем, не отрывая "силой" от их мобильных телефонов. Оказывается, есть готовые учебные сценарии, которые вполне можно развернуть в классе, прямо на уроке математики. C одним из них хочу вас познакомить.
И это продолжение темы Введения в математическое моделирование, которая начата в прошлом посте: Пение сверчка: феномены, процессы, модели
Оригинальная идея для этого урока - от Алекса Овервейка.
Ожидаемые результаты обучения
(по учебной программе Онтарио, описанные в задании):
Ученик способен:
- продемонстрировать понимание отношений, включающих в себя проценты, отношения и единицы измерения;
- продемонстрировать понимание пропорциональных отношений, используя процент, соотношения и коэффициент;
- решать проблемы, используя представление о прямой пропорциональности в различных значимых контекстах;
- продемонстрировать понимание постоянной скорости и ее связи с линейным отношением;
- применять методы работы с данными для исследования отношений между двумя переменными;
- решать проблемы, связанные с пропорциональными зависимостями;
- изображать линейную зависимость и записывать уравнение линии по данной информации.
Оригинальная TeacherDesmos активность Turbo Texter (на английском)
Источники, использованные автором при создании этой активности:
http://mrorr-isageek.com/turbo-texting/
https://cl.desmos.com/t/feedback-on-modeling-activity/380/6
Джон или Кевин?
Пояснения учителя и вопросы к ученикам
Что вы заметили после просмотра видео? Что было интересно?
Ссылка на видео файлы для скачивания
Дайте ученикам несколько минут, чтобы они самостоятельно записали свои идеи. Обмен идеями с партнерами, потом с классом.
Вот несколько вопросов / заданий, которые даются ученикам.
- Какие отношения вы наблюдаете? (Количество символов в тексте, соответствующих времени ввода текста). Ученики постепенно подводятся к принятию решения, были ли эти отношения пропорциональными.
- Создайте эскиз, показывающий, как количество символов в тексте влияет на время создания текста этого сообщения.
- Как этот график выглядит с обоими "текстерами" на одном рисунке?
- Кто самый быстрый? Предсказать, как по вашему эскизу определить, кто быстрее введет текст разной длины Джон или Кевин?
- Кевин заканчивает первым, значит ли это, что он быстрее, чем Джон?
- Как мы будем определять, кто быстрее?
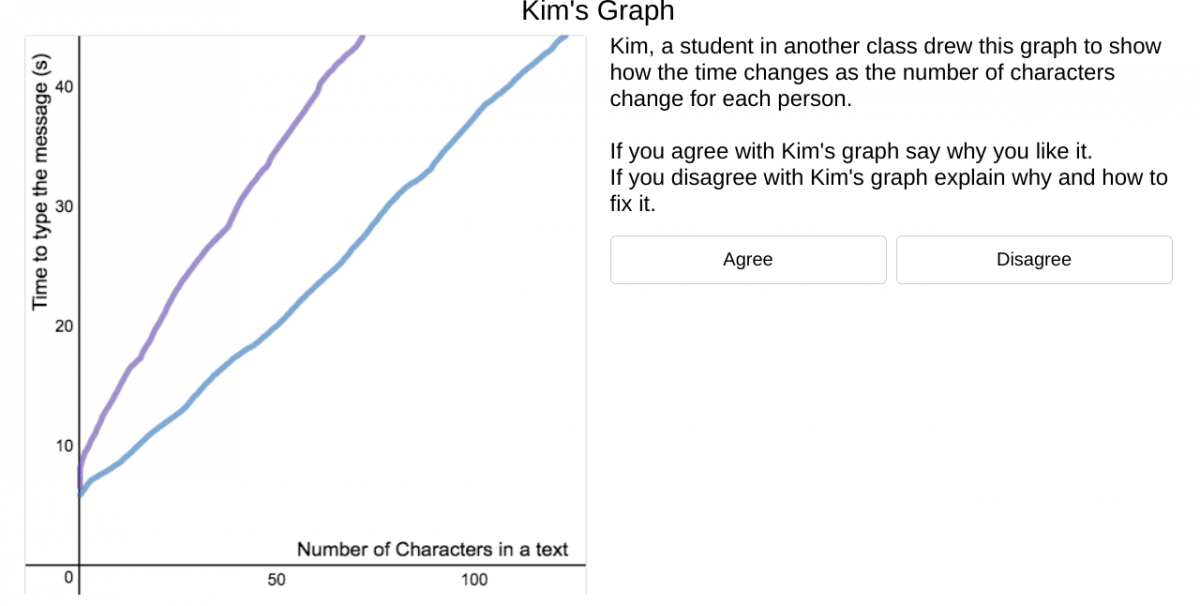
Нужно уделить время этим вопросам, чтобы увидеть и понять взаимосвязь между количеством символов в тексте и временем для его печатания.
Время текстовых сообщений
- Как ученики могут сравнить себя с Джоном и Кевином в отношении скорости ввода текста?
- Попросите их набрать и отправить друг другу сообщения из 165 символов с их телефонов.
- Пусть ученики определят скорость ввода своих текстовых сообщений, чтобы узнать, кто самый быстрый “набиратель текста” (текстер) в классе.
Линейное моделирование
Учитель:
"Теперь вы могли написать это сообщение за 18 секунд, но будете ли вы делать так все время? Сохранится ли тот же темп для более короткого сообщения? А для более длинного?
Или нам лучше продолжить эксперимент для более точных предположений?"
Учитель предлагает ученикам текстовые сообщения разной длины с помощью этого раздаточного материала.
Ученики используют Desmos и инструмент регрессии для создания линейной модели
Инструмент регрессии (инструкция)
Нажать на помощь и выбрать "регрессии"

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных.
Несколько важных пунктов о линейной регрессии:
- Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
- Обозначения интуитивно-понятны.
- Чувствительна к выбросам.
Почитать про метод регрессии
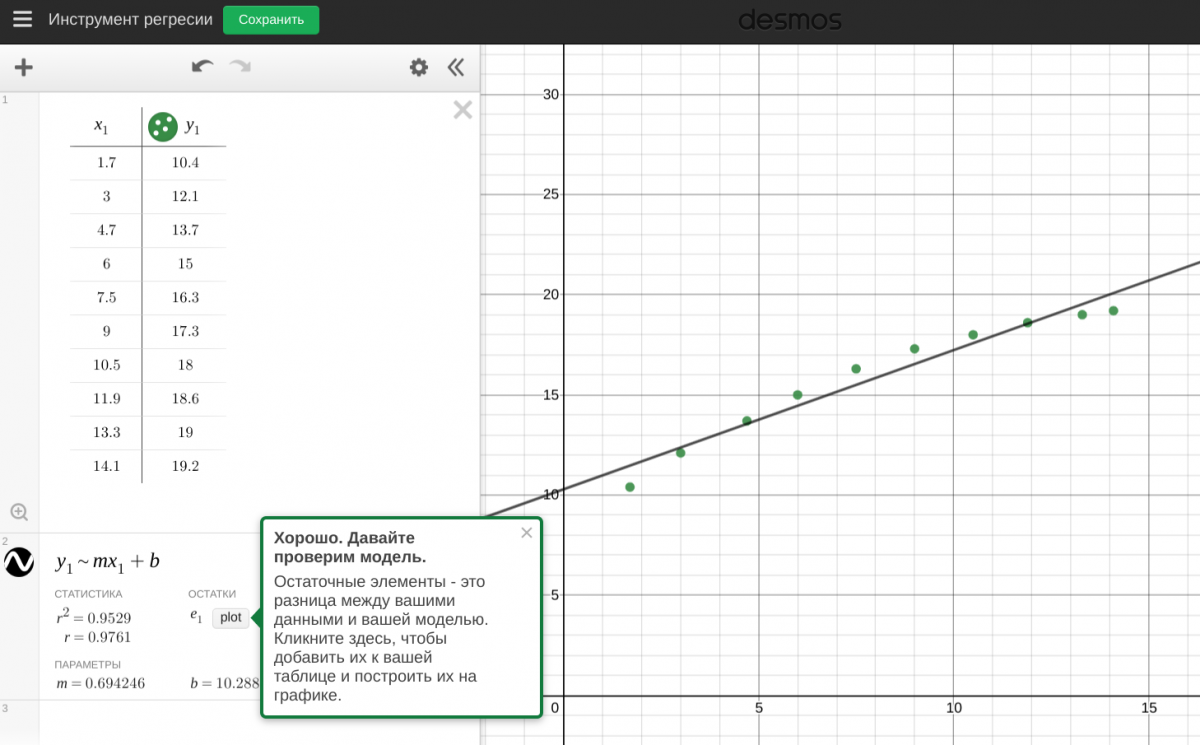
Ученики использовали эту модель для прогнозирования, сколько времени потребуется, чтобы написать 140 символов, 200 символов, а также это сообщение:
«Дорогие мама и папа, я обещаю никогда не писать сообщения во время вождения».
Ученики получают данные для сравнения рассчитанного и фактического времени ввода текста.
Учитель: сравните соотношение между количеством слов в сообщении и временем, необходимым, чтобы ввести текст сообщения. Как изменится уравнение? Это все еще прямо пропорциональная зависимость?
Завершите версию этого упражнения в Desmos
Посты на тему
- Пение сверчка: феномены, процессы, модели
- Мини-исследование в классе: есть ли у вас чувство времени?
- Статистика на карманах




