Обучение, построенное на артефактах и феноменах - что это такое? Интерес к этому большой. Пример в этом направлении нам всем показывают финны, но, оказывается, мы и сами можем многое. Готовясь к вебинару STEAM-проект: от артефакта и феномена к учебной ситуации, искала примеры удачных артефактов, на которых можно было бы развернуть учебную деятельность, вовлекающую учеников. Хотелось артефактов, богатых в плане использования их в качестве подложки для разворачивания важного предметного содержания одного или сразу нескольких школьных предметов.
Мондриан как артефакт
Итак, примером удачного артефакта могут быть картины голландского художника Пита Мондриана. Почему именно он?
- Во-первых, Мондриан - удивительный мастер, чье творчество очень многогранно. Начинал он, как почти любой голландский художник, с рисования коров и мельниц. :) Но стал известен во всем мире благодаря тому уникальному стилю, к которому пришел уже в конце своего творческого пути, когда стал использовать в своих картинах только три цвета (синий, красный и желтый), исключительно прямые линии и простые геометрические фигуры. Благодаря этому особенному стилю он и узнаваем повсеместно! Что касается Голландии, то там можно говорить о настоящей "мондрианомании", в чем могла убедиться сама во время путешествия по городам и местечкам этой страны (см. фото). Но, как оказалось, этот узнаваемый стиль дает пищу для фантазии и творчества не только художникам и дизайнерам.

- Во-вторых, опыт использования картин Мондриана в качестве прототипов для создания цифровых арт-объектов у меня был и свой. Несколько лет назад мы делали с учениками-старшеклассниками проект “Математика и искусство” (об этом здесь Математика и искусство — переплетение возможно!). Много идей здесь: Математика в стиле "мондриан" и "клее"
- В-третьих, в одном из англоязычных образовательных блогов встретилась яркая картинка, которой тут же сама поделилась в профессиональном сообществе учителей математики и информатики. Отклик не заставил себя ждать.
Это был пример артефакта, который мог стать средством вовлечения учеников в обычно скучную учебную работу по форматированию таблиц (речь идет об уроках информатики). Вот эта идея: я кликаю на ссылку и мне достаточно минуты на то, чтобы быстро пробежать текст глазами, потому что идея понятна сразу. И учителя информатики ее тут же подхватывают, едва увидев картинку. Наблюдала это и в своей школе, и в учебном процессе с детьми. Каждый раз эта простая и красивая идея работала с неизменным успехом.
Прямоугольник как "живой объект" математики и информатики
Весь поздний Мондриан - это прямоугольники. У объекта "прямоугольник" в школьной программе по математике, кроме линейных размеров (измерений), есть еще периметр и площадь, которые вводятся через через подсчет клеточек, через математические операции суммы и произведения линейных величин. После того, как ученики начальной школы выучили две формулы для расчетов, эту геометрическую фигуру как бы откладывают в сторону, до тех пор, пока она снова не станет учебным объектом - уже для изучения геометрических свойств прямоугольника и решения задач. Потом, классе в 6-м, ее снова будут рассматривать как одну из фигур класса четырехугольников в рамках общей концепции геометрических фигур на плоскости.
Пока прямоугольник для ученика - неподвижный объект на бумаге или меловой доске, задачи на прямоугольник не очень-то богаты содержанием, подходящим для освоения. Но как только мы помещаем его в систему координат или просто на клетчатое поле, он становится новым объектом интересной для ученика, "живой", математики.
Его размеры можно менять, а форму - ломать и восстанавливать.
Его периметр и площадь становятся функциями, заданными на его линейных размерах как на переменных. И эти функциональные зависимости можно воспринимать не только визуально, но "пощупать" руками, отследить в динамике.
А еще, изменяя в интерактивной среде взаимное расположение сторон и величины углов в динамическом объекте, ученики могут сами исследовать геометрические свойства любой фигуры. Причем не заучивать и запоминать, часто не понимая сути, а предсказывать и открывать для себя.
А если поместить прямоугольник в таблицу (Excel или таблицы Google) или, например в какую-то из сред визуального программирования - он становится объектом информатики. Такой вот ход!
Суть в том, что в специальных средах объект прямоугольник можно подвергать дополнительной трансформации: поворачивать, перемещать, разрезать на части, снова складывать из элементов. И все это - простым движением мыши или нажатием кнопки.
То есть, динамическй объект можно всячески изменять и переделывать - возиться с ним (англ. to tinker).
А мы, имея возможность отслеживать действия ученика в цифровой среде, выявляем его понимание через способность ученика применять освоенные инструменты, объяснять и интерпретировать объекты, изменять объекты и параметры, самооценивать свою работу.
Как на цветных прямоугольниках Мондриана развернуть предметное содержание начальных курсов математики и информатики?
Подумалось, что весь Мондриан - вообще потрясающий артефакт, на нем одном можно построить целый мини-курс математики класса для 4-5-го и, частично, для 6-го. Какие темы можно охватить?
Математика
- Геометрические фигуры и построения
- Преобразования на плоскости
- Площади
- Периметры
- Части, дроби
- Координаты на плоскости
- Моделирование: масштаб, разметка
Информатика
- Форматирование таблиц
- Адреса ячеек и диапазоны в таблицах
- Визуальное программирование в PencilCode. Пример Мондриан (6 класс), Мондриан (9 класс)
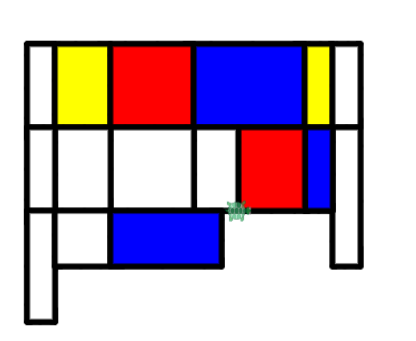
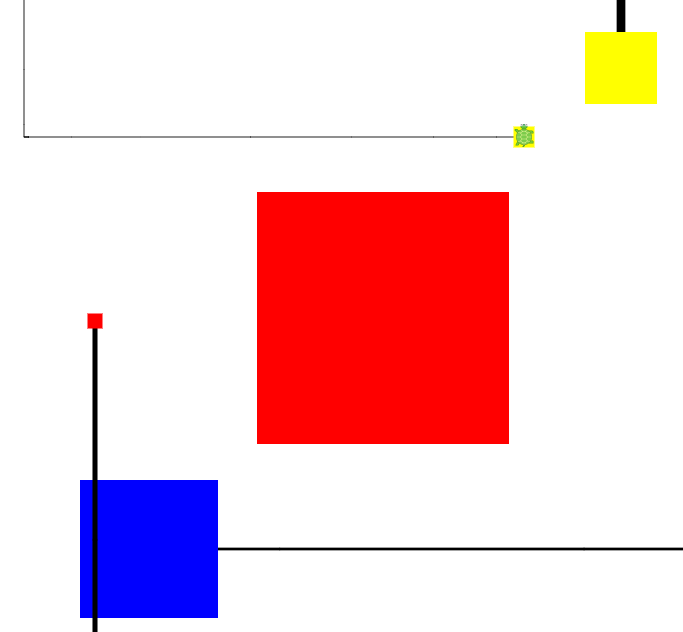
- Интерактивные игры и викторины в Scratch
- Схемы и алгоритмы
- Создания динамических картин в GeoGebra на примере картин Мондриана (старшая школа 10-11 класс) Апплет1 Апплет 2
Пример учебной активности, построенной на артефакте
Вот пример интегрированной активности по двум предметам (математике и информатике) в среде https://teacher.desmos.com/. По математике она охватывает темы периметров и площадей прямоугольников. По информатике - адреса ячеек и диапазонов в таблицах. При том, что, проходя активность, ученики применяют изученное ранее на уроках, во многих заданиях им еще надо дополнительно справиться с новым интерфейсом, приспособиться к нему, а значит, использовать имеющиеся знания в непривычной ситуации.
Мы разработали эту активность в сотрудничестве с учителем информатики и математики нашей школы Анной Осипенко.
Активность по математике и информатике, 4-5 класс
В этой публикации подробнее хотела бы рассмотреть только три последовательных задания из этой активности. Они устроены интересным образом. Остальные предлагаю проанализировать самим.
Задание-матрешка. Возможность возиться с объектом.
Приведу пример серии из трех заданий, которое вложены в друг друга как матрешка:
-
В первом нужно, воспользовавшись образцом - картиной Мондриана, сделать модель картины с помощью подвижных прямоугольников. Для этого ученику необходимо мысленно разметить имеющееся в распоряжении клетчатое пространство (справа). Линейные размеры не так важны, важнее пропорции и относительное расположении фигур. Отличительная черта этой учебной задачи в том, что нет никаких особенных инструкций по использованию инструментов: ученик должен сам для себя открыть возможность перемещать точки и менять положение и размеры объектов на клетчатой плоскости. В то же время, он имеет возможность самостоятельно проверять правильность своей модели, визуально сравнивая ее с образцом (слева). У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами.
-
В следующем задании нужно определить и корректно записать диапазоны некоторых из полученных прямоугольников, которые оказались встроены в таблицу. (информатика). Благодаря возможностям сервиса teacher.desmos на следующем слайде ученик может работать со своей собственной моделью: она оказывается встроенной в слайд с новым заданием.
-
Новая, третья, задача - посчитать площади этих же прямоугольников. Так организовано, что прямоугольники оказываются встроенными в прямоугольную сетку, на которой выполнить задачу гораздо проще.
Данная активность была использована в работе с учениками 5-ти пятых классов TKVG в конце декабря 2018 года. У нас была возможность проследить, как справляются ученики с заданиями такого типа. В частности, нас интересует описываемое задание на моделирование.

Варианты выполнения задания учениками, есть над чем подумать...
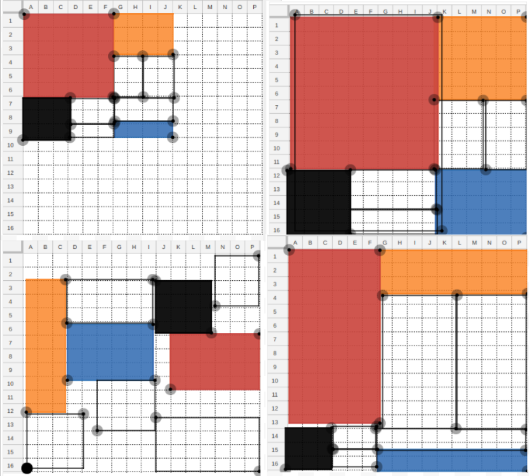
В приведенной активности вы найдете несколько других идей, как использовать данный артефакт в качестве геометрического объекта. Эти идеи - об обнаружении учеником некоторых свойств объектов, а еще о самостоятельной пробе в работе с динамической средой. Особенно интересен прием лупа (о нем есть планы написать позже, анализируя этот и другие примеры).
Разумеется, эту активность можно дорабатывать, широко используя возможности динамической среды. Поэтому было бы интересно увидеть развитие темы в профсообществе.
Есть ли у вас подобные примеры геометрических артефактов, которые бы могли вдохновлять на создание живых объектов математики и информатики? Таким, с которыми ученик мог продуктивно повозиться?
Ссылки по организации смешанного обучения в предметной области математики
- Учителям математики нужен новый подход
- Может ли школьная математика стать STEM-образующим предметом?
- Новая стратегия преподавания школьной математики: "умная бумага"
- Стрельба по мишени, или Цифровые инструменты организации мышления на уроке математики
- STEAM-математика: Почему так важны какие-то ползунки?
- Ремикс-проект начинается с рамы
- STEAM-проект: от артефакта и феномена к учебной ситуации (презентация)
- "Черный ящик" среды цифрового обучения?
- Мини-исследование в классе: есть ли у вас чувство времени?
Cтатьи по STEAM/STREAM проектам
- Математика и искусство — переплетение возможно!
- Математика в стиле "мондриан" и "клее"
- Математика и абстрактное искусство в STREAM-проекте
- Идеи в духе STEAM: геометрический конструктор на основе рисунков Google
- Идеи в духе STEAM: PicassoHead как конструктор
- Постер как форма упаковки информации в STREAM-проекте: Колдер и Вазарели
- STEAM-проект: генератор Кандинского и другие интерактивные апплеты в GeoGebra
- STEAM-проект: черный квадрат Малевича в Desmos и GeoGebra
- STEAM-проект: треугольник в GeoGebra, как получить картину?
- STEAM-проект: мозаики Эшера в GeoGebra
- STEAM-проект: задачи на картинах
- Паркеты и площади в Desmos
- STEAM-проект: снежинка Коха, треугольник Серпинского и другие фрактальные объекты в GeoGebra
- STEAM-проект: по спирали!
- Рисуем мандалы в GeoGebra, или Чудо поворотной симметрии
- Урок виртуальной кройки: клетка, полоска, узор…
- Русский авангард и другие художники в Desmos
- Как привести солнце в движение, или Послесловие к виртуальной выставке
- МК "Другая математика с Desmos": измени апплет и научись!

