К нам на наш Desmos-курс пришли участники, что называется, с хорошим кругозором... Их самостоятельные работы, которые они создают и публикуют в таблице на каждом этапе, открываешь с любопытством: что там интересного на этот раз?
Обо всем на онлайн-мастерских и курсах не расскажешь, всему не научишь... При этом всегда ждешь от них еще чего-то, что даже сам в него не закладывал, Поскольку один из принципов таких курсов, как наш, — обмен идеями и продуктами, то они (идеи) как правило, рождаются прямо в процессе обучения. Частенько случается выход на новые темы, как и на новые типы задач. Это тоже - один из прогнозируемых результатов онлайн-обучения в группе.
Об одном из таких открытий хочу рассказать в этой публикации. Его автором стала участник нашего курса Наталья Крамарчук. Задачи, предложенные Натальей и визуализированные ею в Desmos, идут в тексте под номерами 3 и 4.
Остальные подобрала "на лету" и воплотила в апплетах Desmos, чтобы развить эту замечательную, на мой взгляд, идею.
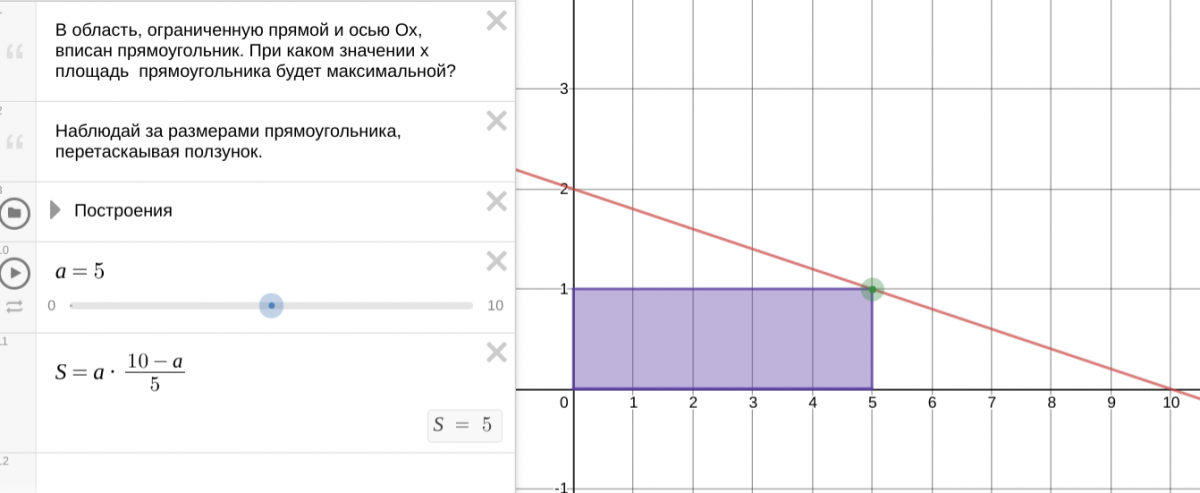
Задача 1. В область, ограниченную прямой и осью Ox, вписан прямоугольник.
В область, ограниченную прямой и осью Ox, вписан прямоугольник. При каком значении x площадь прямоугольника будет максимальной?
Условие и решение задачи в desmos-апплете
Задача 2. В область, ограниченную параболой y=c-x^2 и осью Ox, вписан прямоугольник
В область, ограниченную параболой y=16-x^2 и осью Ox, вписан прямоугольник, стороны которого параллельны координатным осям и одна сторона лежит на оси Ox. Определить наибольшую площадь прямоугольника.
Источник условия задачи https://clck.ru/KGKkf
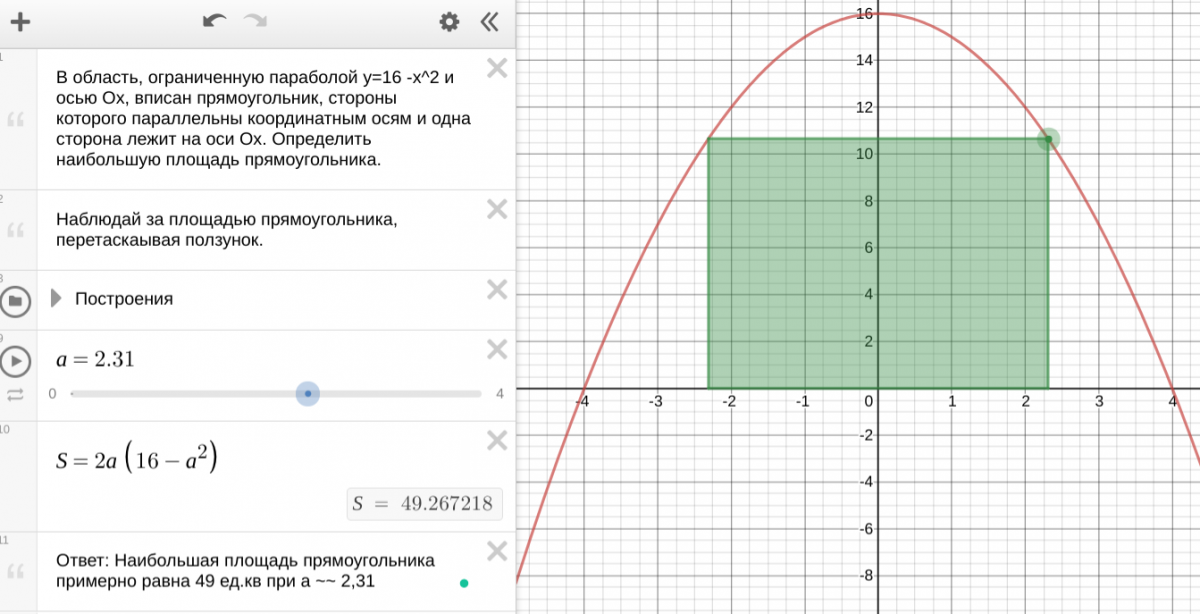
Условие задачи в Desmos-апплете. Решение с помощью ползунков.
Задача 3. Максимальная сумма площадей фигур в прямоугольном треугольнике.
Дан прямоугольный равнобедренный треугольник АВС с катетом АС=1. Точки К и L лежат на АС и ВС соответственно, при этом KL параллельна АВ. KN и LM - перпендикуляры на АВ. Пусть СК=х, S1 - площадь треугольника KCL, S2 - площадь треугольника AKN.
Источник условия задачи: "Дидактические материалы по геометрии." В.И.Рыжик и А.А.Окунев
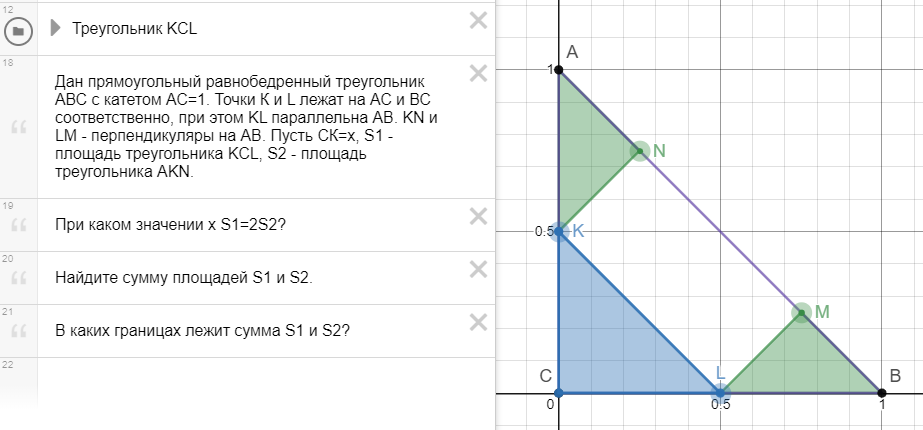
Условие задачи в Desmos-апплете с помощью ползунков Условие от Крамарчук Натальи.
Решение от Людмилы Рождественской
Задача 4. Суммарная площадь двух кругов
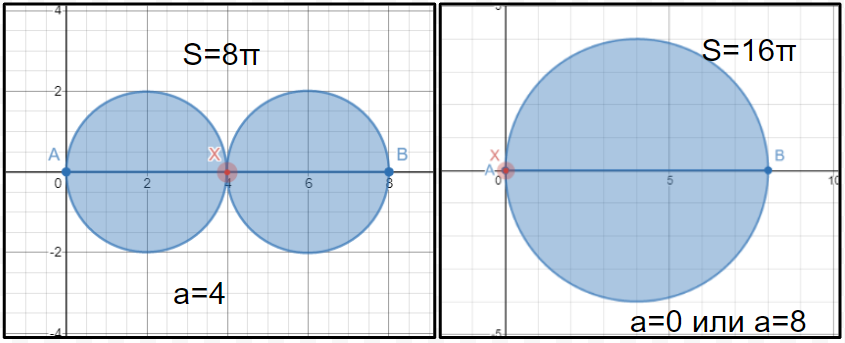
На отрезке АВ выбирают любую точку Х. В каких границах лежит суммарная площадь двух кругов с диаметрами АХ и ВХ.
Источник условия задачи: "Геометрия. 8 класс." А.Д.Александров и др.
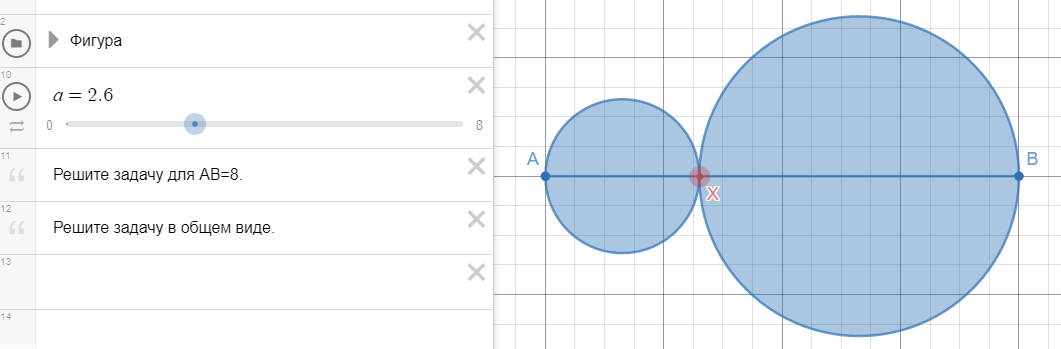
Условие задачи в Desmos-апплете с помощью ползунков
На картинке предельные положения ползунка для наименьшей и наибольшей суммы площадей кругов.
Задача 5. "ОКНО"
Окно имеет форму прямоугольника, ограниченного сверху полукругом. Периметр окна равен P. Определить радиус полукруга a, при котором площадь окна является наибольшей.
Источник условия задачи https://clck.ru/KGKkf
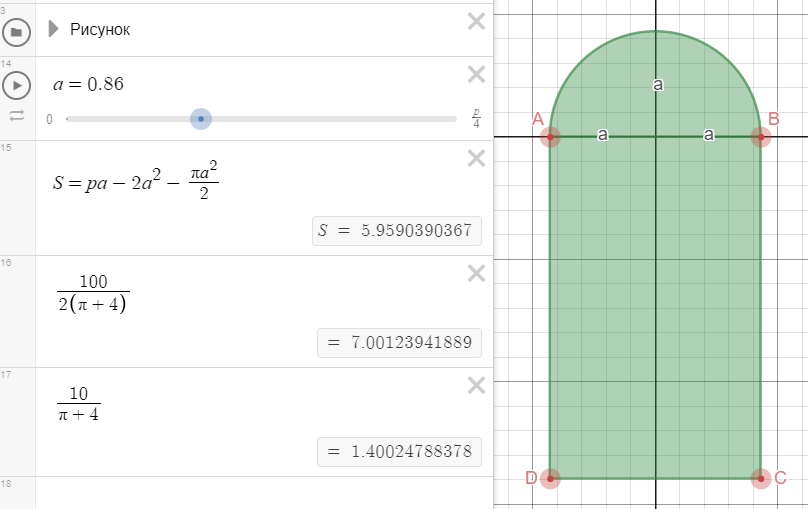
Условие задачи в Desmos-апплете. Решение с помощью ползунков
Задача 6. Треугольник, отсекаемый на осях
На координатной плоскости в первой четверти задана точка С(a,b). Провести через эту точку прямую, отсекающую треугольник наименьшей площади, ограниченный данной прямой и осями координат.
Источник условия задачи https://clck.ru/KGKkf
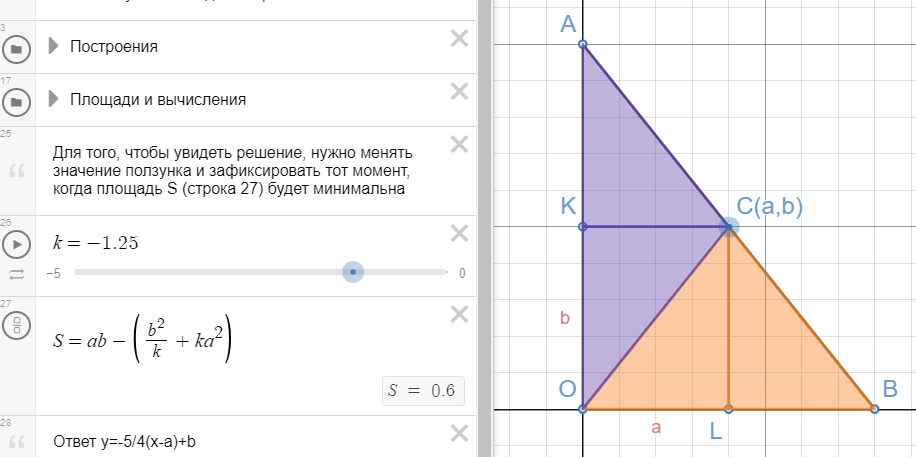
Условие задачи в Desmos-апплете. Решение с помощью ползунков
Фермер и загоны
А вот эту задачу нашла готовой, только перевела на русский ее условие.
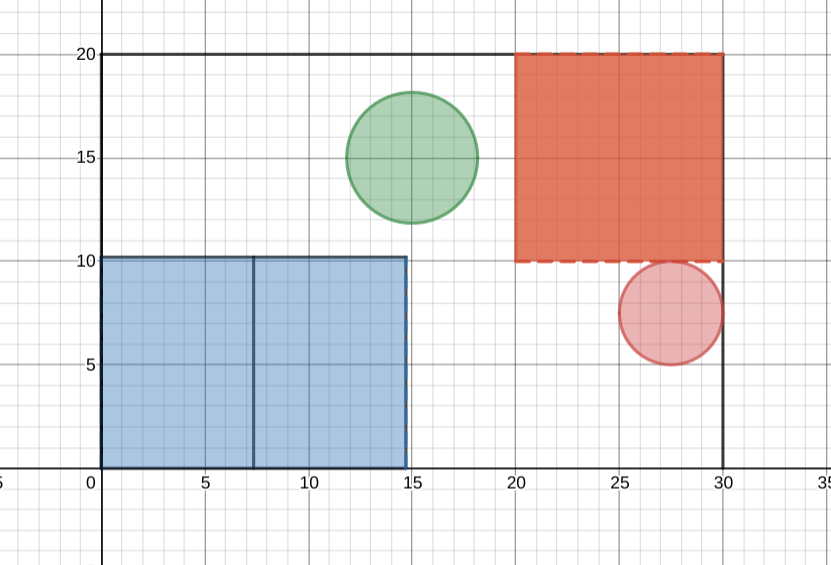
Для чего можно использовать подобные апплеты?
Как знают все учителя математики, задачи на оптимизацию решаются с использованием первой и, если необходимо, второй производной. Чем же здесь могут быть полезны desmos-апплеты?
- Во-первых, и это главное использование - для визуализаций подобных задач путем создания динамического чертежа. В таком чертеже наглядно видны те предельные состояния, которые ученикам часто бывает трудно представить "в уме".
- Во-вторых, многие задачи так, действительно, можно решить - с одним ползунком, без производной. Не все, конечно, но многие. Да, и конечно, решение будет приблизительным, поскольку в "настоящем" решении ответ часто записывается иррациональным выражением, а калькулятор нам выдаст лишь его округление. Тем не менее...
Процесс создания таких апплетов тоже по-своему труден: чтобы чертеж "получился", нужно правильно ввести переменные, выразить одну или несколько из них через какой-тот один параметр, задать для этого параметра-ползунка корректные границы интервала.
🌱 Нужно задать вычисляемую функцию формулой - через этот параметр.
🌱 И, конечно, придумать, как ученик сумеет зафиксировать то значение ползунка, при котором функция имеет экстремум (минимум или максимум).
🌱 Но зато - это будет "геометрическое" решение. Без необходимости считать производную, хотя #Desmos и это может.
Что скажете, коллеги?
Публикации по теме
- Идеи заданий с подвижными отрезками
- Виртуальный геоборд своими руками
- От бумаги к цифре: утренние ремиксы
- Мондриан как артефакт
- Ремикс-проект начинается с рамы
- Клетчатая Ёлка и новогодние ремиксы
- Математическая задача как вызов. Уроки в Desmos
- Инструкция: как создать "объект в зеркале" в среде Desmos
- Курс Desmos-математики стартовал!
- Математики больше не плачут, они анализируют проблемы
- Polygon: от подвижных геометрических фигур до картин
- Страсть к кругам и окружностям
- Задачи на оптимизацию — с помощью ползунков Desmos
- О "Розе ветров" и других визуализациях-ремиксах в Desmos
- По следам курса Desmos-математики: бери и делай!