Известно, что 5х5=25, а 6х6=36.
Это математики очень хорошо придумали - такое удобно и легко запомнить.
Но почему тогда и 7х7 не сделали равным 47?!
Трудно было что ли?)
И как вообще правильно: как удобно или как правильно? Или...
И вы уже, конечно же, догадались, что далее в статье речь пойдет о красоте.
О красоте понимания.
Наверняка многие с детства помнят обложку тетрадки в клеточку.
Я с математикой познакомился еще до школы и поэтому, глядя на эту обложку, испытывал некоторое удивление: к чему такие сложности - это раз, и почему это называется таблицей - это два?
На сборник простых примеров еще тянет, а вот на полноценную таблицу, как-то не очень.
А вот это похоже на таблицу уже больше.

Таблицу, давно и очень удачно придуманную товарищем Пифагором, но до сих пор еще весьма далекую от совершенства. И мы попробуем сейчас ее доработать. Кстати, на этой обложке тоже не обошлось без ошибок. Правильное ее название: таблица умножения и деления.
Но давайте разбираться по-порядку. Началось все, когда я взял в руки длинный деревянный брусок, пилу-ножовку и превратил его в целую кучу деревянных кубиков.

Тут же набежали строители и начали эту беспорядочную кучу кубиков раскладывать и упорядочивать.





Начали как водится с простых линейных рядов.
Но скоро они уже перестали помещаться в кадр фотоаппарата.

Чтобы кубики не убежали из кадра мы тогда начали нарезать ряды на одинаковые куски и складировать (складывать) их.


Можно так, а можно такое же количество сложить и эдак.


В результате пришли к прямоугольнику. Прямоугольник уже можно крутить как угодно, количество составляющих его кубиков от этого не меняется.
Самыми красивыми из прямоугольников являются квадраты. Это, наверное, потому, что они сами на себя при повороте похожи.
Начинаем собирать квадраты.






Ух, ты! А тут уже кажется квадратная формула какая-то закономерная напрашивается.
Но не будем отвлекаться на формулы, мы ведь просто в кубики играем.
Следующей стройкой у нас на очереди оказалась лестница.




История сохранила не все кадры постройки лестницы, да это и не важно.
Тут самое главное сама идея - лестница, ведущая вверх.

Мы живем в мире, где царствует сила тяжести. Преодоление ее есть наша (человеков) основная задача.
Поэтому Правильную Таблицу Умножения, надо сделать также растущей вверх. И лучше всего будет, если каждый построит эту свою таблицу умножения своими собственными руками. Так он точно ее никогда не забудет.
Таблицы ближайшие родственницы столов (table). История стола-таблицы восходит к столам денежных менял на торговых рынках. Именно они первыми догадались разделить поверхность обычного стола на ячейки.
Я тоже возьму обычный лист бумаги и сделаю из него таблицу, разделив его на ячейки. И стану заполнять его растущими числами-прямоугольниками по определенным правилам. Начну с заселения диагонали квадратами.








Нетрудно заметить, что диагональ - ось симметрии таблицы, и вовсе не обязательно вычислять всю таблицу, достаточно ограничится вычислением треугольника под диагональю, а потом просто отобразить его симметрично на другую сторону относительно оси.
Если под рукой вдруг не окажется листа бумаги, не беда, можно последовать примеру древних шумеров и воспользоваться куском глины, предварительно раскатав его в лепешку.

Для тех же читателей, кому уже исполнилось 21 год рискну предложить еще одно изображение таблицы Пифагора и соответствующую моменту цитату из лекции известного американского физика Ричарда Фейнмана.
Он был поэт, он говорил (с):
"...«Весь мир в бокале вина». Мы, наверное, никогда не поймем тот смысл, который он вкладывал в эти слова, ибо поэты пишут не для того, чтобы быть понятыми. Но, бесспорно, что, внимательно взглянув в бокал вина, мы поистине откроем целый мир. В нем и физические явления (искрящаяся жидкость, испарение, меняющееся в зависимости от погоды и вашего дыхания, блеск стекла) и атомы (о которых нам говорит уже наше воображение). Стекло - это очищенная горная порода; в его составе кроются секреты возраста Вселенной и развития звезд. А из какого удивительного набора реактивов состоит это вино! Как они возникли? Там есть закваска, ферменты, вытяжки и разные другие продукты. Ведь в вине скрывается большое обобщение: вся жизнь есть брожение. Изучая химию вина, нельзя не открыть, как это и сделал Луи Пастер, причины многих болезней. Сколько жизни в этом кларете, если он навязывает нашему сознанию свой дух, если мы должны быть столь осторожны с ним! Наш ограниченный ум для удобства делит этот бокал вина, этот мир на части: физику, биологию, геологию, астрономию, психологию и т. д., но ведь природа на самом деле никакого деления не знает! Давайте же и мы сольем это воедино, не забывая все же, что мы увидели. Пусть этот бокал вина доставит напоследок еще одно наслаждение: выпить его и обо всем позабыть!.."

И что, скажите, можно еще к этому добавить?)
Добавить к этому можно только одно.
Мы получили в свое распоряжение крайне удобный, концентрированный и интуитивно понятный (т.е. понятийный) инструмент, представляющий из себя ячеистую, пространственную, хорошо визуализированную структуру.
В которой можно легко ориентироваться при помощи координатной сетки, в качестве которой можно использовать такой бумажный уголок.
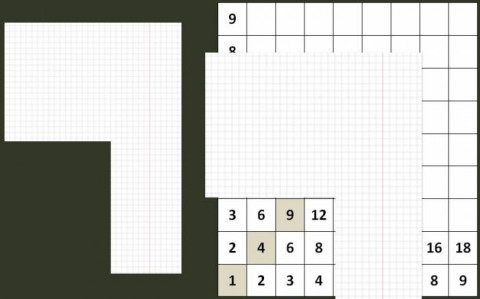
Таблицу легко разместить так, чтобы она всегда была перед глазами. При многократном использовании запоминание ее произойдет само собой.
Таблица должна стать тем же, чем она была изначально - помощью в работе.
Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.
При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение - это всего лишь многоКРАТНОЕ сложение, и соответственно деление - это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений "на сколько больше/меньше" и во сколько раз больше/меньше". Это очень важно для последующего составления уравнений по условиям задач.
Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение - мать учения) и самостоятельного выявления такой закономерности.
Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой. Подобно Журдену из "Мещанина во дворянстве" Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.
Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.
Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.
Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия - это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа - это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот - смотря что удобнее.
Понимание графиков с осями Х и Y, названиями "абсцисса" и "ордината" уже не вызовет затруднений - это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И... объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).
В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги - площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.
И все это закладывается заранее всего лишь одним шагом - Правильной Таблицей Умножения.
И к тому же, в нашем же распоряжении для работы с таблицами есть очень удобный инструментарий будь то Ecxel от мелкомягких или его аналог гугл-таблицы от Гугл.
Конечно, электронная таблица не так наглядна, как, например, ментальная карта, зато легка в освоении, удобна и всегда под рукой. А нарочитая условность прямоугольников ячеек легко запускает мотор воображения.
Табличный процессор необычайно мощный, гибкий и полезный инструмент для широкого круга задач.
И в заключение хочу выразить особую благодарность Игорю Юрьевичу Шкурину, собственно с подачи и из общения с которым в свое время и родились материалы этой статьи.
Спасибо за внимание!
Продолжение следует.
________________________________________________________________________
Другие статьи автора:
1. В хоккей играют настоящие мужчины.
3. Волшебная лампа мейкера Ала-Джина.
5. Приходите тараканы, я вас чаем угощу.
8. По следам одного школьного проекта.
10. Десакрализация гаджета или вскрытие покажет.
13. Угольный микрофон или усилитель из резистора.
14. Угольный микрофон для ленивых. Часть 2.
15. Айда к нам!)
16. Курс в курсе.
18. Отчет по курсу "Кухня непрофессионала".
19. Создание мультов в Power Point.
20. О бедном герконе замолвите слово.
21. Вечный тормоз.
22. Как мы учили собаку лаять.
24. Клуб ЖелДорМод.


