Этой темой заинтересовалась не так давно, обнаружив интересное приложение для браузеров и планшетов. И тогда же сделала небольшой пост-сборку Задачи для геоборда. В нем описывались задания для геодоски, в основном, для начальной школы.
Но, оказалось, что может быть хорошее продолжение при изучении самых разных тем по геометрии и в средней школе.
Темы, в которых могут быть использованы геоборды (геометрические доски):
- Площадь прямоугольного треугольника
- Площадь треугольника
- Площадь 4-х угольника
- Построение 4-х угольников с заданными свойствами
- Длина отрезка (введение в понятие иррационального числа)
- Теорема Пифагора
- Развивающие задачи на построение и преобразование фигур на квадратной сетке
Поделюсь несколькими полезными активностями в среде teacher.desmos, переведенными с английского, дополненными и адаптированными.
В этой активности учащиеся используют Geoboard для нахождения длин отрезков и практики в применении теоремы Пифагора.

Исследование площади треугольника на геоборде
В этом упражнении учащиеся используют геоборд для изучения треугольников и их площадей.

Challenge Creator
Здесь ученики будут создавать свои СОБСТВЕННЫЕ задачи и решать задачи от своих одноклассников. Мы рекомендуем ученикам завершить оставшуюся часть задания, прежде чем приступить к задаче. Мы ожидаем, что создатель Challenge Creator добавит 30 минут к продолжительности занятия.
Поощряйте учащихся решать задачи друг друга, но также уделите время тому, чтобы проанализировать ответы на свои собственные. Используйте панель управления учителем, чтобы найти уникальные задачи и уникальные решения, которые могут расширить понимание вашими учениками математики. Выделите их для студентов, а также спросите их, чему они научились из своего опыта.
Мы стремимся сделать это социальным и творческим опытом для учеников. Мы рекомендуем вам подчеркивать это всякий раз, когда вы проводите такую активность в своем классе.
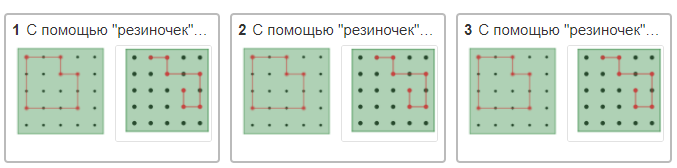
Способы нахождения площади на сетке
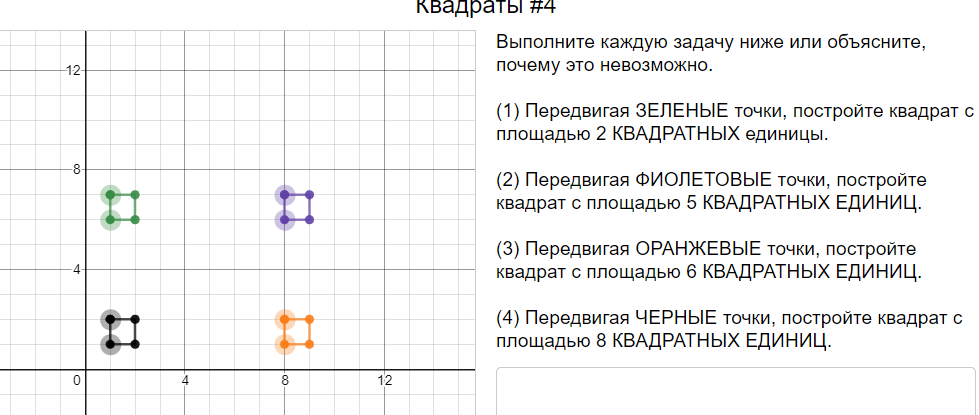
В этой активности учащиеся строят квадраты в целочисленной решетке, определяя длины их сторон. Используйте это как введение в иррациональные числа или как прелюдию к теореме Пифагора. Эта готовая и переведенная на русский оригинальная активность от Desmos имеет интересную конструкцию: в первом задании ученику предлагается построить квадрат, в следующем за ним - проанализировать, как он пришел к своему решению. Для технического воплощения такой возможности в редакторе teacher.desmos предусмотрена возможность "встраивания" того решения, которое найдет любой ученик, в следующий экран.
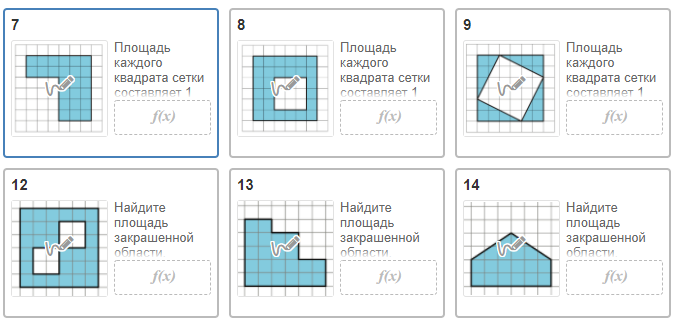
Цель активности состоит в том, чтобы ученики поняли, как упростить радикалы, изобразив квадрат и длину его стороны. Алгебраические правила разрабатываются, и к концу упражнения предоставляются случайно сгенерированные вопросы для проверки понимания. Обратная связь и проверка правильности встроены.

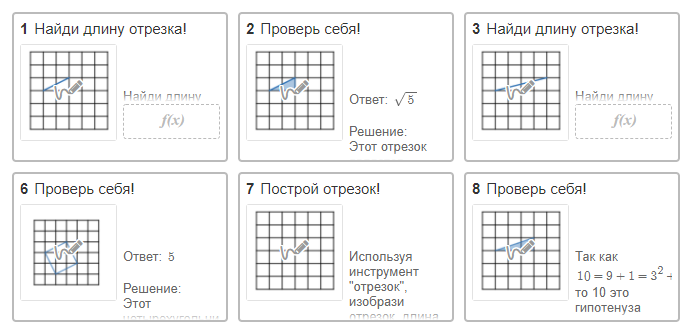
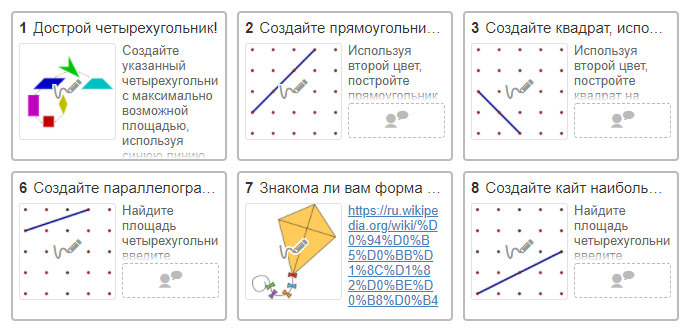
В этой активности ученики строят отрезки, треугольники и четырехугольники заданной длины или площади, используя теорему Пифагора. Все задания даны на клетчатой бумаге с клеткой 1х1, что позволяет не использовать никаких инструментов, кроме линейки ("отрезок"). Идея возникла в процессе использования книги В.А. Смирнова и И.М. Смирновой "Геометрия на клетчатой бумаге" http://biblio.mccme.ru/node/2130/shop
В этой активности ученики по одной стороне достраивают четырехугольник с наибольшей возможной площадью и указанными характеристиками. Эта задача требует от ученика понимания определений разных видов четырехугольников, а также является отличным введением в тему параллельных и перпендикулярных прямых. Инспирировано постом Don Steward
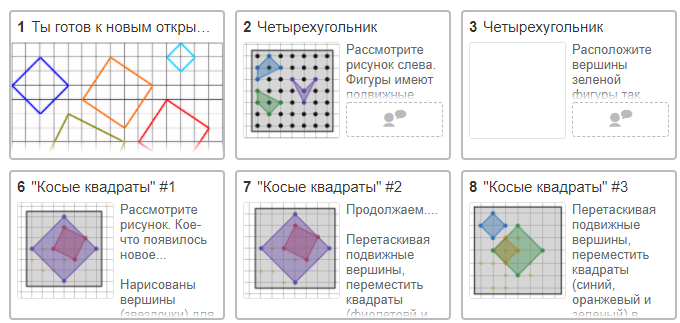
Практикуемся с "косыми квадратами"
Идея заданий с "косыми квадратами" на бумаге взята в сообществе Мышематика https://www.facebook.com/mousemath/posts/2461972550691943. Для подвижных чертежей использован desmos-файл https://www.desmos.com/calculator/90knjh6peu (автор Александр Шевчук).
Пазлы Zukei для четырехугольников и треугольников (Идея головоломки и ее название принадлежит Наоки Инаба (Naoki Inaba)
В каждой из этих головоломок нужно соединить три или четыре красные точки зеленой ломаной, чтобы получить необходимую фигуру.

О своем опыте использования таких активностей упоминала в посте Уроки математики в гибридном формате.
Что скажут коллеги? Накопился ли уже опыт использования этих активностей?
Помогают ли геоборды осваивать ученикам перечисленные выше темы?
Статьи по теме
- Идеи заданий с подвижными отрезками
- Виртуальный геоборд своими руками
- От бумаги к цифре: утренние ремиксы
- Мондриан как артефакт
- Ремикс-проект начинается с рамы
- Клетчатая Ёлка и новогодние ремиксы
- Калейдоскопы как ремиксы
- О "Розе ветров" и других визуализациях-ремиксах в Desmos
- Polygon: от подвижных геометрических фигур до картин
- Страсть к кругам и окружностям
- Списки? А для чего они нужны? Потренируемся?


