Людмила Рождественская • 4 января 2021

Desmos-метаморфозы: как превратить снеговика в цветик-семицветик

лайков: 6

Как музыканты слышат музыку, читая ноты, так математика может научить видеть цифровые объекты через их записи формулами.

Как этому научиться? Можно, например, предлагать ученикам такие задания в которых требуется "записать" этот самый объект, восстановить его запись по визуальному изображению.

А можно, наоборот, попробовать просто "рисовать функциями". Хотя, скорее, это конструирование, сборка из деталей. Один совсем свежий пример...

Снеговик не из привычных "шаров", а из "комов"

Снеговиков в Desmos "рисуют" (собирают) обычно с помощью уравнений окружности, для закрашивания используя неравенства. Таких, например, или вообще, клетчатых, но все равно, из "шаров".

Поэтому, размещенный в сообществе Signum cнеговик, сделанный как-то по-другому, привлек мое внимание. Захотелось разобраться, а как это устроено. Автор этого снеговика Александр Шевчук.

Составные части снеговика - комы - "нарисованы" с помощью комбинации операторов distance, с которыми я не очень до этого была знакома. Сам по себе он совсем не сложен, но не хватит никакого воображения, чтобы "увидеть", какие необычные фигуры может порождать их комбинация (сумма или произведение).

image-20210104122610-2

Элементы фигуры через точки настройки и оператор distance

Небольшой экскурс в тему оператора distance...

Desmos. Оператор distance. Автор Александр Шевчук:

..многие знают, что distance это упрощенная форма расчета расстояния между двумя точками по теореме Пифагора. Но тем не менее, у него расширенная форма синтаксиса и некоторые интересные особенности применения. В тело оператора можно вставлять не только координаты конкретных точек, но и точку с координатами в виде переменных "x" и "y". В приведенном макете это точка g= (x,y). Таким образом можно численно-графическим способом решать системы уравнений в теме оптимизации.

Проблема в том, что таким образом нельзя получать расчетные численные значения и можно ориентироваться только на график. Но и это полезно для понимания динамики математических процессов. Если решать практические задачи, то выставляя маркерную точку при помощи масштабирования, можно получить координаты с точностью до девятого знака после запятой. Даже космические корабли с такой точностью не отправляют в полет. И конечно можно создавать фигурки для рисования.

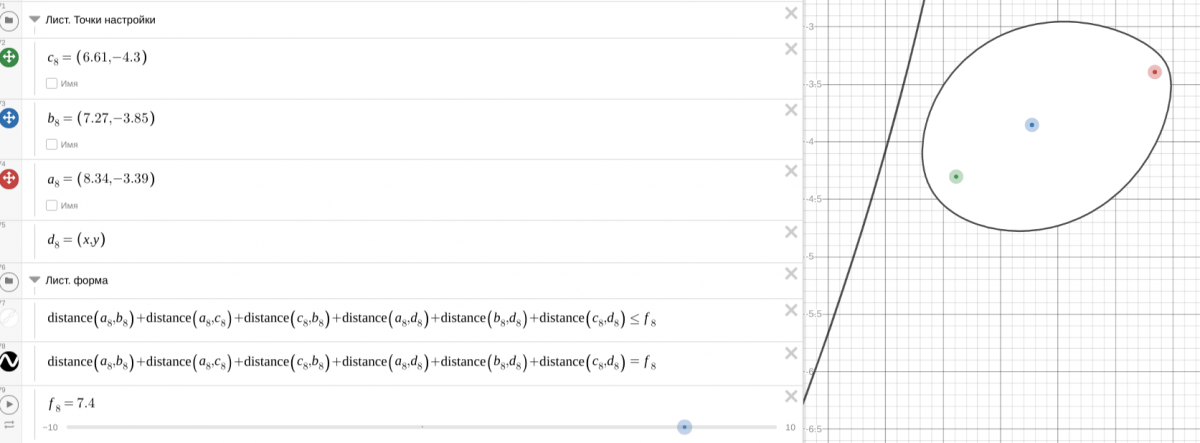
Заглянув в папки с названиями элементов, обнаруживаем, что каждый "снежный ком" задается 4-мя точками настройки (из них 3 точки с числовыми значениями и 4-ая, координаты которой заданы переменными).

Форма "кома" лепится парой условий: одним уравнением (для контура) и одним неравенством (для заливки цветом).

Меняя положение подвижных точек настройки, вы можете менять форму элементов, вернее, тремя точками и ползунком f в папке. Они сделаны видимыми:

Файл Снеговик 21 с открытыми папками и точками настройки элементов фигуры

image-20210104122954-3

Превращение снеговика в цветик-семицветик. Работа с формой.

Но что делать с готовым снеговиком? Просто смотреть на него?

Чтобы понять, как это устроено, можно разобрать объект на части, а потом попытаться собрать из этих частей какой-то свой, новый, объект.

Такой объект придумался как "цветик-семицветик". Почему именно он? Какая связь снеговика с цветком? Может быть, потому, что "комов" в снеговике оказалось ровно семь? И еще всплыло в памяти задание для первоклашек по теме, которое делала когда-то давно, правда, с помощью совсем других инструментов.

В процессе обдумывания задачи, возникали вопросы:

Как мне передвинуть все комы в нужное место и сдвинуть их к какому-то общему центру - нового объекта - цветка?
Как изменить форму кома на форму лепестка?
Как дорисовать еще один ком-листок?
Как дорисовать стебель?

Отвечая на эти вопросы и меняя что-то в записи формул, удалось постепенно все проблемы решить. Очень выручала подвижность точек настройки, которые можно было просто перетаскивать мышкой. В остальном требовалась только аккуратность в именовании переменных для лепестков (по две папки на каждый объект).

По готовым лекалам с помощью точек настройки наконец собрала цветик-семицветик, пока не раскрашенный.

Цветик-семицветик. Не раскрашенный

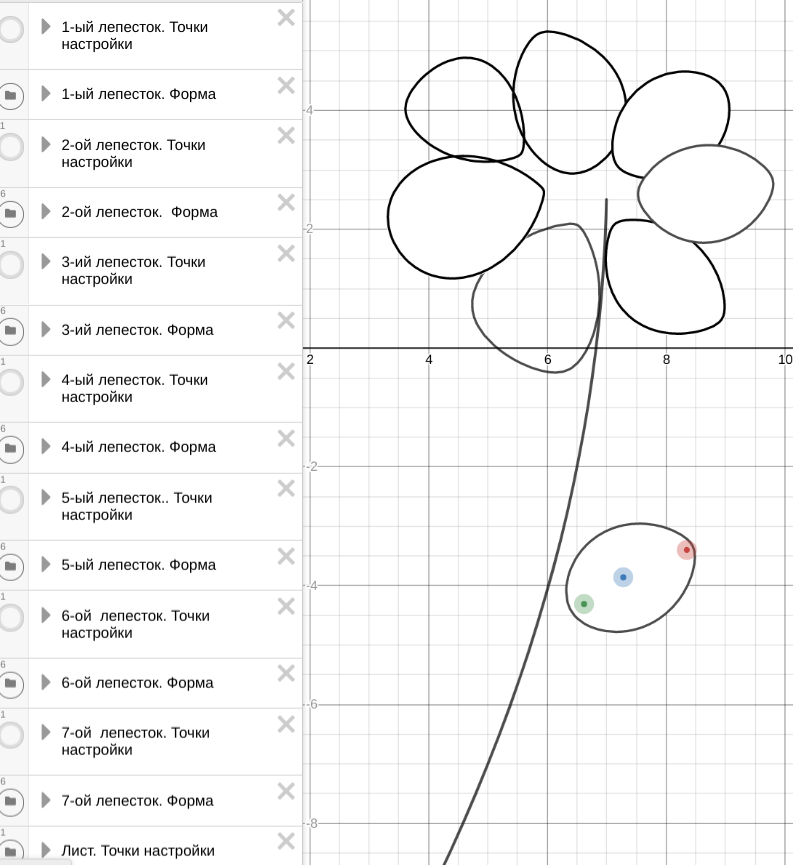
image-20210104153432-2

Как рисуется лист и стебель с помощью готовых форм и уравнений (неравенств)

Тут все будет ясно по картинкам. Листик создан ровно теми же двумя папками с тем же набором точек и функций.

image-20210104153614-1

Стебель задан параболой, видимой на отрезке:

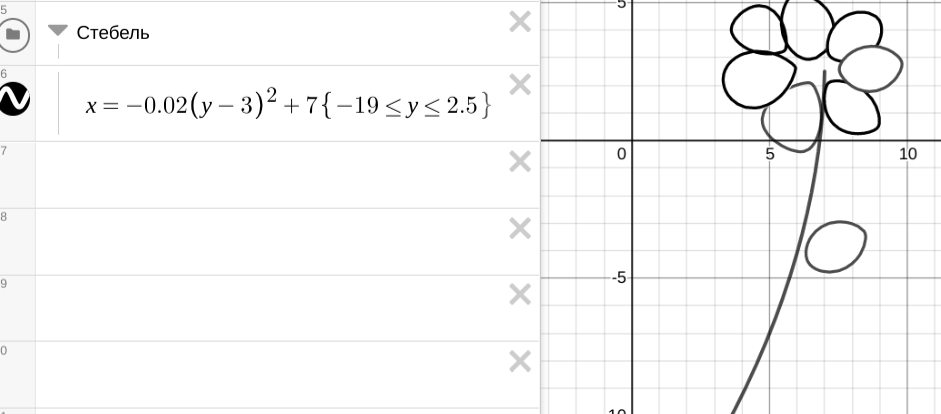
image-20210104155720-1

Раскрашиваем цветик по схеме КОЖЗГСФ

Для раскраски нужны были 7 "чистых" цвета для окрашивания лепестков, как в оригинальной сказке.

Расшифровка этих цветов известна всем из курса средней школы:

КОЖЗГСФ - Каждый Охотник Желает Знать, Где Сидит Фазан. Вот вам и цветик-семицветик.

Осталось подобрать rgb-кодировку цветов.

Например, красный запишем с помощью оператора h_{1}= rgb(255,0,0)

image-20210104154742-2

Остальное предлагаю разобрать самим читателям:

Цветик-семицветик-2001 rgb

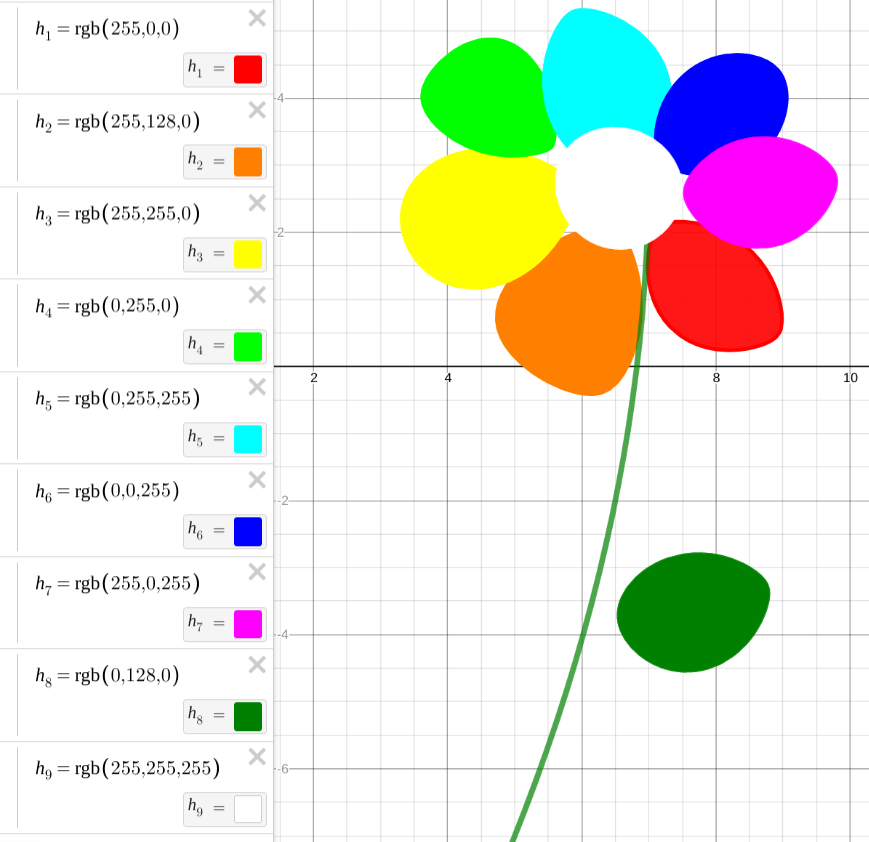
image-20210104153317-1

Таким образом, из форм снеговика в Desmos сделала цветик-семицветик. Недостающие для листика и центра цветка формы создала по прототипу.

Потом отдельно решала задачу с раскраской лепестков.

И теперь (и это самое главное), у меня теперь есть задачка для учеников по раскрашиванию его лепестков в чистые цвета по схеме: КОЖЗГСФ.

Добавление в программу смены цветов для лепестков

Как тему развил Александр, записав чередование цветов с помощью списков!

Цветик-семицветик-2001 rgb. Смена цвета Версия Александра Шевчука

Вроде, теперь к этому файлу добавить нечего? А вдруг...

Присоединяйтесь!

P.S.

Этот пост - попытка рассказать о процессе обмена знаниями, именно так, не просто файлами... Хотя со стороны могло и как-то по-другому показаться, наверное. С огромной благодарностью к Александр Шевчук,

который стал настоящим инициатором этого поста.