Настоящее понимание, как может быть организован учебный процесс в STEM и STEAM-подходах приходит, когда сталкиваешься с хорошими образцами учебных сценариев или тем, что мы называем лучшими практиками.
Эти образцы при всей непохожести друг на друга не произвольны, они имеют свою структуру и логику. Усиленные акценты в учебной деятельности, организуемой по таким сценариям, делаются на самостоятельной переинтерпретации учениками ситуации из того первоначального вида, с которым они знакомятся, с последующим ее "проигрыванием" по правилам какой-либо из предметных дисциплин.
Задачи такого типа называются "жизненными проблемами", их включение в учебную работу возможно на любой из возрастных ступеней (в предлагаемых примерах от 12 до 19 лет). И, как правило, они предполагают использование знаний из нескольких предметных областей: математика, биология, физика, химия, инженерное дело.
Рассмотрим пример, который, впрочем, совсем не нов. Но его особенность - наличие распознаваемой учениками жизненной проблемы, которую необходимо перевести в модель.
Это первая публикация с примером к статье: Смешанное обучение на уроках математики: каким оно быть НЕ должно?
" Если вещь не будет интерактивной, ее сочтут сломанной."
Кевин Келли, «Неизбежно. 12 технологических трендов»
На полпути к модели
Ученики, пытаясь формализовать проблему, перевести ее на язык схемы и переменных, - только на полпути к модели. Построить сразу хорошую интерактивную модель самостоятельно ученикам бывает трудно. Кроме навыков создания чертежей, использования важных в контексте задачи понятий и введения необходимых переменных и функций, нужно владеть неким набором базовых инструментов для работы в динамических средах. Здесь хорошим подспорьем могут стать готовые интерактивные модели, построенные в современных графических калькуляторах desmos и geogebra. Ученики могут играть с этими моделями, работать с их элементами и параметрами, изменять их и отслеживать результаты изменений.
Пример: проектирование парковочного въезда в подвальный гараж
Источник http://www.fisme.science.uu.nl/toepassingen/28297/
Лицензия CC BY-NC-SA 4.0
Аннотация
Цель этой задачи - облегчить въезд на парковку с улицы в подвал различных типов автомобилей и других движущихся объектов, таких как детские коляски, инвалидные коляски и т.д. Естественное намерение: сделать переход с улицы в подвал как можно короче. Эта задача навеяна (и является продолжением) "проблемы парковки", предложенной командой Mascil of Spain. Задача реализует математические идеи в контексте строительства дорог, проектирования автомобилей, архитектуры, управления движением (лежачие полицейские). Ожидается, что ученики изучат реальную ситуацию с помощью моделей и среды динамической геометрии. На основе экспериментов они улучшают свою интуицию по отношению к рассматриваемой ситуации, формулируют и проверяют гипотезы и, наконец, находят практически приемлемые решения.
Простая модель: машина-черепашка
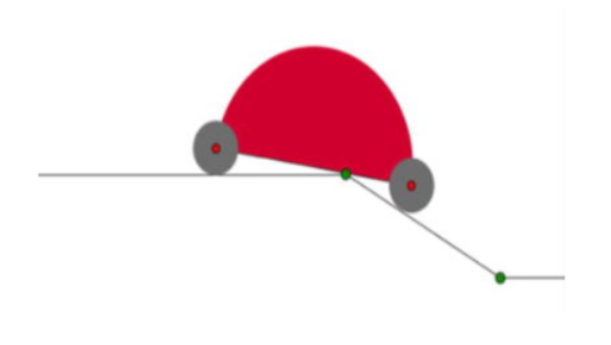
Вводные для ученика: Вы - архитектор, и ваша задача - облегчить парковочный въезд с улицы в подвальный гараж. Для этого вам необходимо спроектировать прямолинейный уклон, соединяющий улицу и подвал-гараж недавно построенного дома, как показано на рис. выше.
Динамическая модель в GeoGebra (упрощенная модель автомобиля)
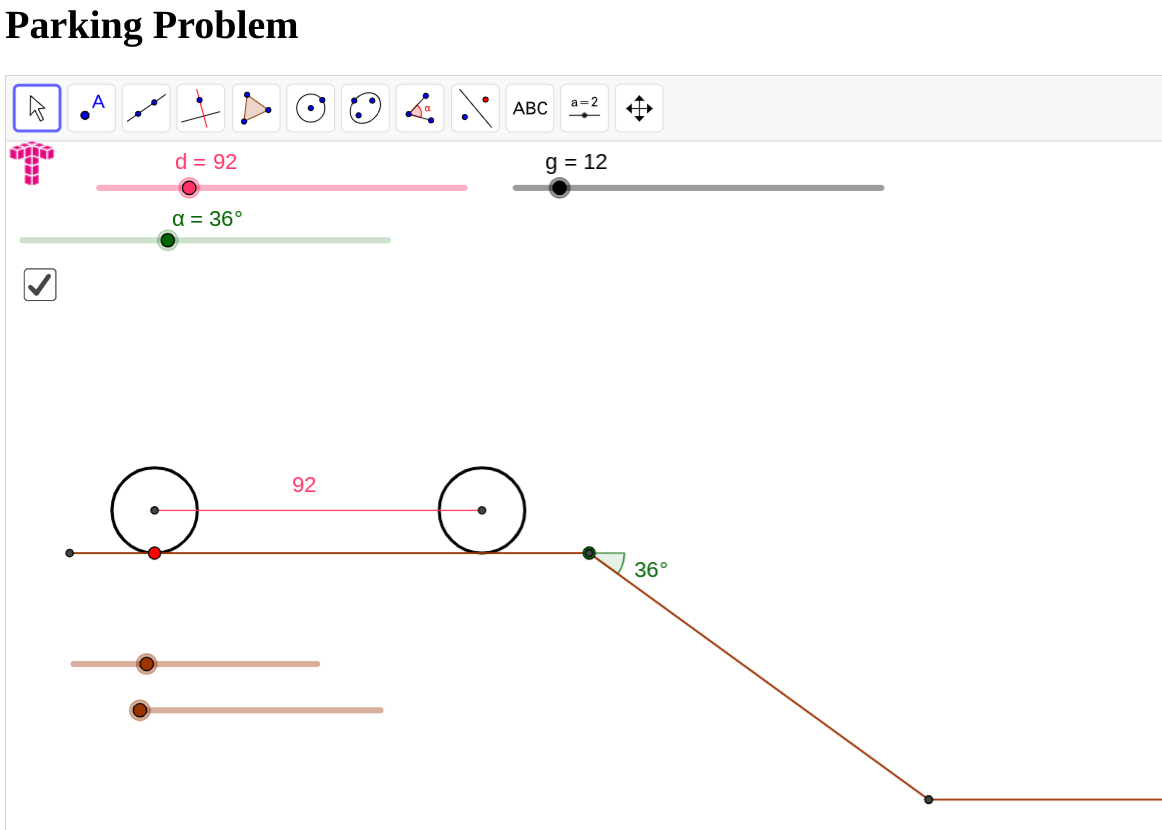
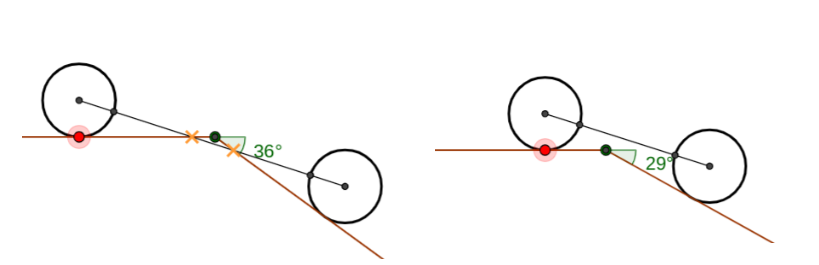
Исходы испытаний могут выглядеть так: 1. Уклон не преодолен. 2. Уклон преодолен благополучно.
Переменные и ползунки, сколько их нужно?
Модель в таких задачах - не статична. Нам потребуется ее тестировать, меняя значение переменных. Введение в модель любой переменной сопровождается введением ползунка. Это означает, что придется позаботиться об области определения для каждой переменной - ползунок всегда работает на конкретном заданном отрезке. Первоначально эти, крайние значения, подбираются из условия и, часто, "здравого смысла", а если что-то пойдет не так, границы ползунков всегда можно подобрать поточнее уже в процессе.
Большой плюс описываемой ниже открытой задачи - довольно большой, но при этом ограниченный набор переменных.
Это переменная для угла уклона и две переменные для продольных "габаритов" автомобиля.
d - расстояние между осями колес
g - радиус колес
α - угол уклона для съезда
Введены также дополнительные (неименованные) ползунки для изменения некоторых линейных размеров конструкции самого съезда. Они находятся снизу в апплете. Для решения задачи в грубом, первом приближении, эти переменные могут быть не существенны, но вводя их в нашу модель в виде управляемых ползунков, мы оставляем ученику возможность самому сделать необходимые допущения о том, с какими переменными он будет работать.
Что с динамической моделью делают ученики?
Дальше разработчиками предложен план для проведения последовательности тестов на динамической модели.
В первой части ученику нужно взять конкретные предложенные значения переменных-ползунков (на деле, установив их в нужное положение). И, перемещая модель автомобиля за подвижную точку, протестировать, проедет ли автомобиль опасное место, не повредив своего кузова.
Задание 1.
Если колеса автомобиля-черепахи имеют радиус 8 см, а расстояние между центрами колес составляет 72 см (как показано на рисунке 2), сможет ли автомобиль-черепаха безопасно преодолеть уклон
?
Второе задание организовано в виде таблицы уже для трёх испытаний автомобилей разных размеров (см. ниже).
Задание 2.
Есть три автомобиля-черепахи разных размеров, как показано в таблице:
Автомобиль-черепаха
Радиус
колес
Расстояние между
центрами колес
TC1
8 см
72 см
TC2
10 см
99 см
TC3
13 см
111 см
Какой самый крутой склон, который могут преодолеть все три автомобиля-черепахи?
На следующих шагах (3-4) ученики ученики исследуют максимально допустимые значения какой-либо одной из трех переменных при фиксированных значениях двух других.
Далее перед испытателями ставится задача (5) найти максимальное расстояние между центрами колес (фиксированного радиуса), для которого еще возможна парковка. В «момент касания» нужно измерить угол между днищем автомобиля-черепахи и горизонтальной линией.
Последующие, постепенно усложняющиеся, задания смотреть здесь: ᷾Рабочий лист для ученика
Усложнение модели
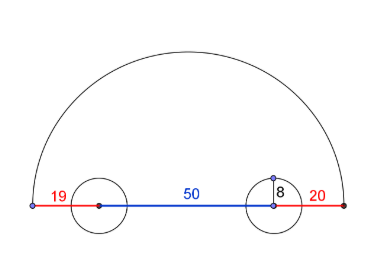
На более поздних этапах испытаний появляются новые переменные для описания модели машины, обозначающие линейные размеры выступающих передних и задних частей автомобиля-черепашки. Здесь появляются новые проблемы преодоления съезда, возникающие при выходе из склона и входе в подвал.
Усложнение динамического "стенда" в Geogebra для модели машины, более близкой к реальной, может быть новой, более трудной задачей, к которой, однако, ученик уже более подготовлен на предыдущих этапах.
Динамическая модель в GeoGebra (усложненная модель автомобиля)
.....
Модель, близкая к реальному автомобилю
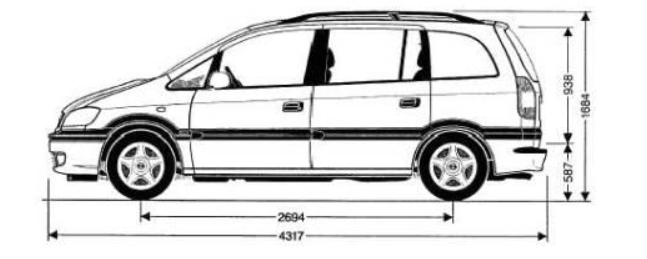
На следующих этапах габариты автомобиля могут быть усложнены до автомобиля какой-то из существующих марок (с реальным расстоянием между землей и низшими частями автомобильного шасси). После знакомства с текстом из Википедии обсуждается вопрос "почему нельзя просто увеличить это реальное расстояние (клиренса - дорожного просвета)?" (Статья на русском), (статья на английском, полнее и лучше в контексте задачи).
Дальше тема может быть развита в проблему преодоления "лежачих полицейских" на суперкаре.
См. «Наихудший враг суперкара - лежачий полицейский» https://www.youtube.com/watch?v=GSUU5xOMAU8.
Чем отличается такой способ организации обучения от традиционного?
Решать такую задачу, имея для подмоги лишь статичный бумажный рисунок, невозможно. Обычно задачи похожего плана рассматриваются в курсе математики старшей школы, когда ученики изучили тему "производные функций" и познакомились с так называемыми "задачами на оптимизацию", которые как раз решаются с использованием производных. Почему нельзя применить этот метод для рассмотрения данной проблемы? Например, потому что в школе обычно ограничиваются рассмотрением функций одной переменной, а здесь их, как минимум, три даже в упрощенной модели.
Но то, что нельзя или очень сложно сделать на бумаге, можно красиво сделать в цифре. В итоге ученики овладевают одной из техник работы с данными в цифровой форме.
И почему, собственно, нужно откладывать рассмотрение таких "жизненных проблем", рассчитывая на более старший возраст учеников, если с помощью динамических моделей это можно сделать гораздо раньше? Только нужно осознавать, что это несколько другая математика.
И понимание "про феномены и артефакты" при таком способе обучения точно полнее. Что думаете?
Использованные ресурсы
Полезные ссылки на ресурсы по STEM-образованию
- Mascil (Mathematics and science for life)
- Future Classroom Lab (FCL)
- Future Classroom Lab (Resources)
- Wonderville - канадский сайт для учителей естествознания, работающих в STEAM-подходе
Ссылки по теме "Цифровая среда для изучения математики"
- STEM - STEAM - STREAM на смену предметам и предметникам...
- Может ли школьная математика стать STEM-образующим предметом?
- "Черный ящик" среды цифрового обучения
- Стрельба по мишени, или Цифровые инструменты организации мышления на уроке математики
- Новая стратегия преподавания школьной математики: "умная бумага"
- STEAM-математика: Почему так важны какие-то ползунки?
- Мондриан как артефакт
- Мини-исследование в классе: есть ли у вас чувство времени?
- Статистика на карманах
- Учителям математики нужен новый подход
- Ремикс-проект начинается с рамы
- Клетчатая Ёлка и новогодние ремиксы
- Математическая задача как вызов. Уроки в Desmos
- Редактор активностей в TeacherDesmos: графический калькулятор graph
- Классные активности в TeacherDesmos: инструкция для новичка
- Инструкция: как создать "объект в зеркале" в среде Desmos
- Задача о рулончике туалетной бумаги, или Математические вызовы от мистера Штаделя
- От бумаги к цифре: утренние ремиксы
- Смешанное обучение на уроках математики: каким оно быть НЕ должно?


