Почти год назад на Новаторе был опубликован пост Весы и уравнения о чудесном сервисе, на котором можно решать линейные уравнения и даже их системы в игровом формате. Ученик поначалу, пока не выработал стратегии, тренируясь на простых образцах, даже не будет связывать свои действия с какой-либо математической темой из школьного курса, с переменными, равносильными преобразованиями и понятием тождества. Ему не придется приводить уравнение к каноническому виду... Все, что от него требуется здесь - уравновесить "вешалку". И чему здесь можно научиться? Скажете - бесполезная трата времени?
А вот и нет.
Для тех из наших учеников, у кого резкий переход к абстрактным правилам и преобразованиям обычно сопровождается устойчивой неуспешностью по математике, такая игра может оказаться продуктивным вызовом, предложением испытать себя. Причем, ничем особенно не рискуя... По крайней мере, нет риска получить плохую отметку. Зато есть шанс догадаться до каких-то ходов самому!
В чем идея?
Идея заключается в уравновешивании вешалки-мобиле с развешанными на ней разноцветными фигурами, под каждой из которых "спрятаны" числа. Под фигурами одного цвета одинаковой формы - одни и те же числа. Вот каков простой принцип этой игры. Но, если понимать суть, наши "фигуры" - это переменные. И на каждой вешалке их может быть размещено больше одной. В переводе на математический язык - это аналог линейного уравнения с одной или несколькими переменными. Да, здесь, как и в "стандартном объяснении" темы ученику приходится подставлять числовые значения в цветные фигуры-значки. Но здесь он делает это на интуитивном уровне. Сначала подбором, а потом уже и к составлению уравнений переходя...
Если стало интересно, загляните по ссылке https://solveme.edc.org/Mobiles.html
И, оказывается, этот игровой подход может быть тропинкой к более формализованной математике.
Основанные на принципе "вешалки" появилась первая активности в TeacherDesmos: Уравновесим вешалку. Простые линейные уравнения
(Перевод SmolGU team, студенты Смоленского Государственного университета под руководством преподавателя Анны Самариной).
А интерактивные возможности, заложенные в активности, позволят ученику или самому проверить правильность своих гипотез, или обсудить их с одноклассниками.
Посмотрим на примеры заданий:
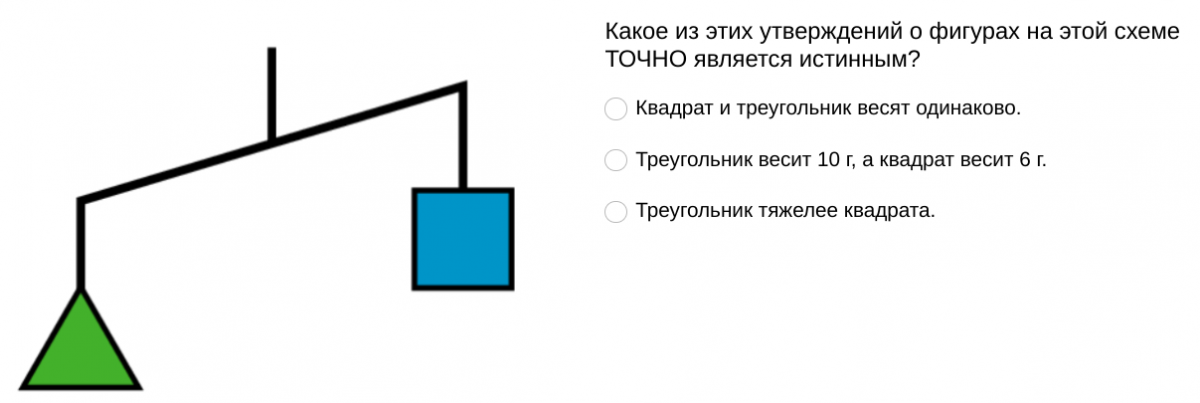
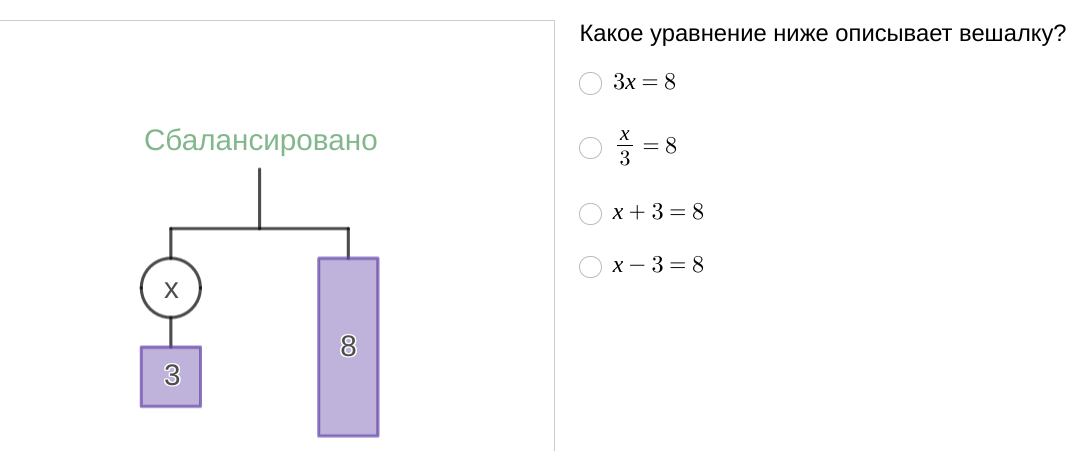
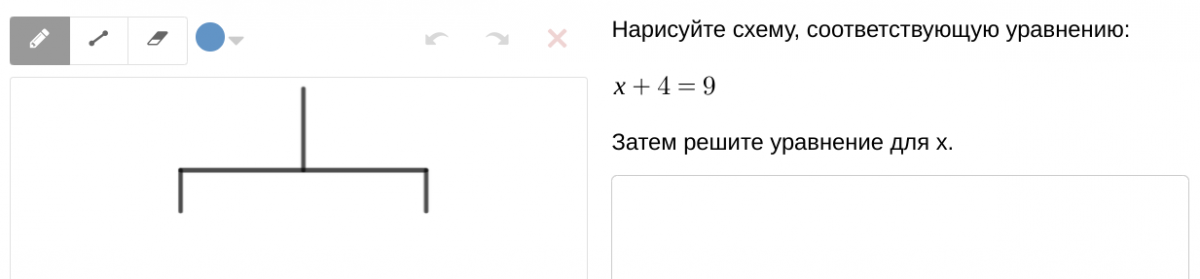
Мы видим здесь движение от схемы - "вешалки" к линейному уравнению с одной переменной, и обратное - от уравнения - к схеме.
Почему бы не использовать столь наглядную схематизацию?
В этих упражнениях продолжается работа по использованию сбалансированной вешалки для разработки стратегий решения уравнений. Ученикам предлагаются сбалансированные вешалки, и нужно написать уравнения, представляющие их. Затем требуется объяснить, как использовать диаграммы, а затем, как составить уравнения, и как найти его решение. Ученики начинают видеть структуру уравнений и диаграмм, находят соответствия между ними, лучше начинают понимать стратегии решения.
Попробуем записать результаты обучения в автивностях с "вешалками" в стандартных формулировках:
Ученик
- может объяснить, что общего у сбалансированной вешалки и соответствующего уравнения.
- может написать уравнения, которые могли бы представить массы объектов на сбалансированной вешалке
- может сравнить выполнение одного и того же действия с грузами на каждой стороне сбалансированной вешалки с решением уравнений. Все это - путем вычитания одинаковой суммы с каждой стороны вешалки или упрощения, например, деления на одно и то же число.
Для формализованной записи использован ресурс
Что обычно изучают в теме "Системы линейных уравнений"?
Давайте вспомним, чему мы обычно учим учеников, проходя темы "Линейные уравнения" и "Системы линейных уравнений" на уроках математики?
- Вводить переменные (в задачах, которые сводятся к решению линейных уравнений или их систем)
- Выражать одну переменную через другую
- Методу подстановки при решении систем
- Методу сложения при решении систем
- Графической интерпретации решения системы двух линейных уравнений
Как правило, мы имеем этот стандартный набор. Но не всех учеников, к сожалению, получается научить этим действиям.
Возможно, не хватает наглядности?
Три примера типовых задач, которые обычно (на бумаге) решают по-другому
Задача 1
7 шоколадок дороже чем 8 пачек печенья. Что дороже – 8 шоколадок или 9 пачек печенья?
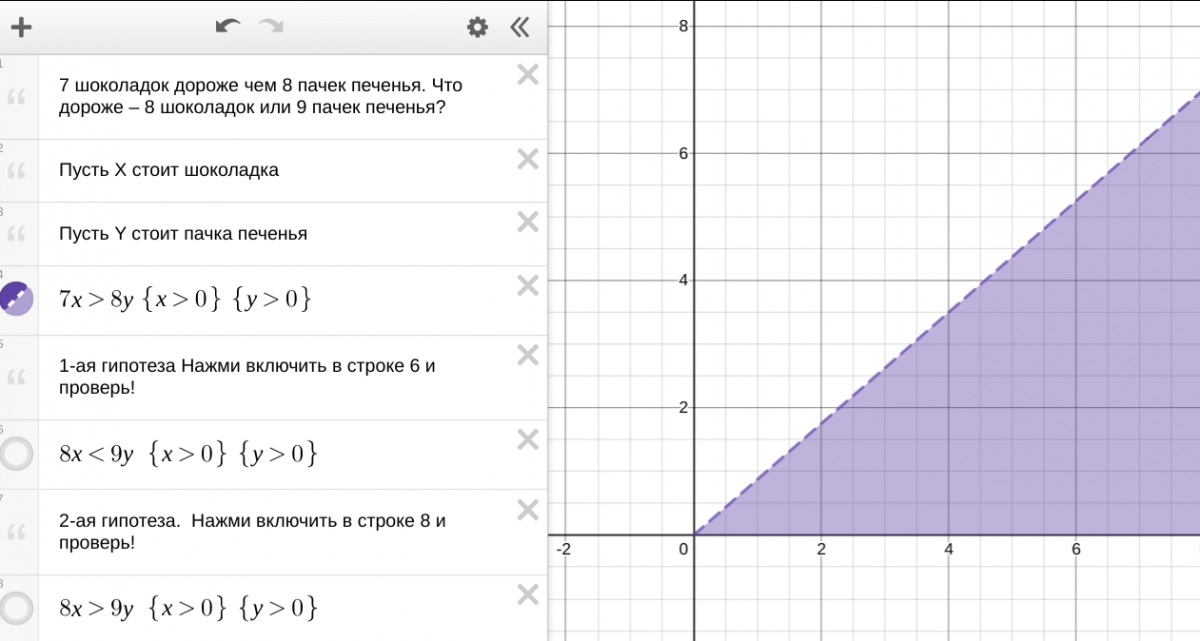
Задача 2
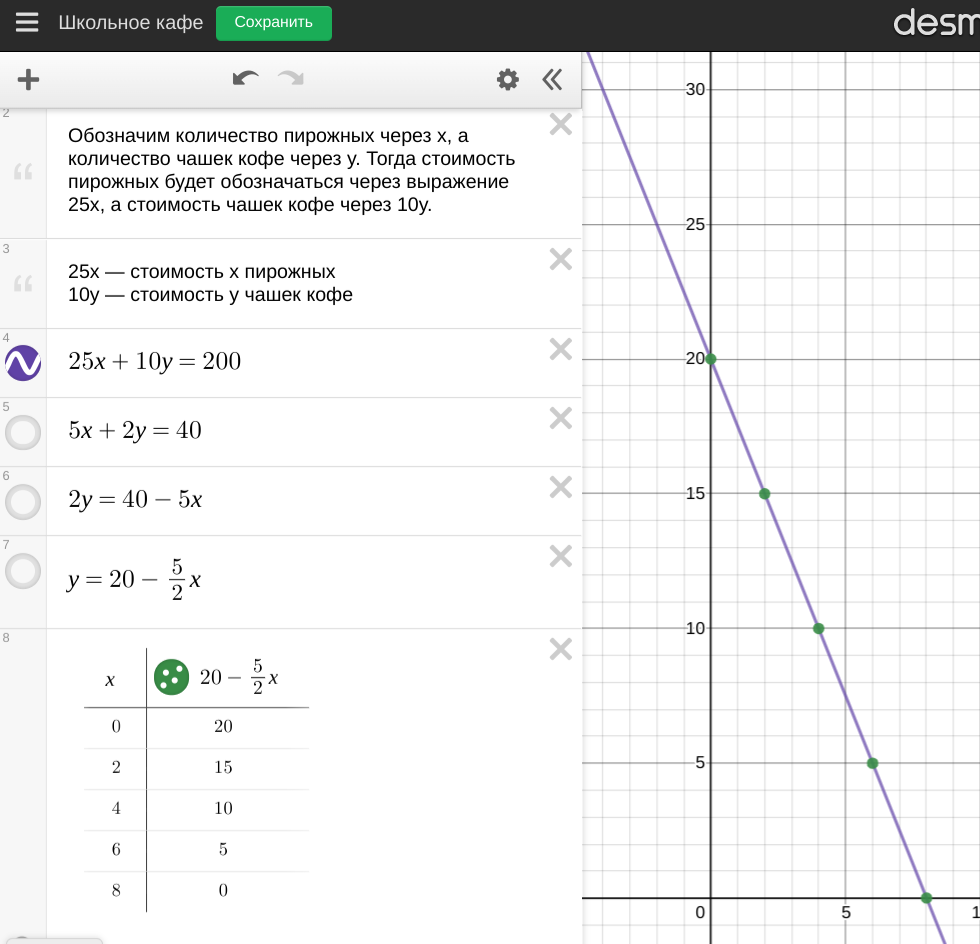
У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?
Задача 3
«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»
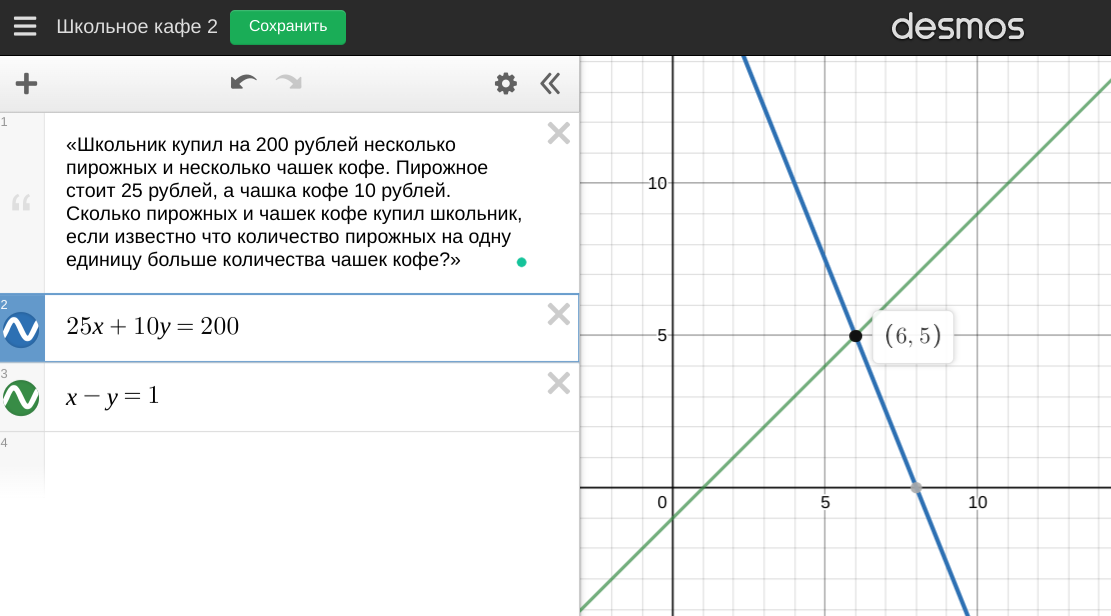
Все три задачи на бумаге решались бы стандартными способами сводящимися к составлению уравнений, неравенств или их систем, а также подходящим методам их решения.
В Desmos эти решения визуальны, калькулятор как бы решает задачу "за ученика"...
Но тогда получается, что нужно учить учеников при переводе задачи на язык математики записывать ее так, чтобы калькулятор смог нас "понять" . И чтобы те данные, та информация, которые калькулятор нам "вернет", также были очевидными и наглядными.
И как это решение, которое выдаст калькулятор, разглядеть, понять, интерпретировать?
Умеем ли мы это? И делаем ли?
Цифровые инструменты организации мышления
А теперь пример такой активности, в которой учебная деятельность по теме развернута совершенно по-другому. Она не про стандартные приемы, она - про выдвижение гипотез, выбор способов, их обсуждение....
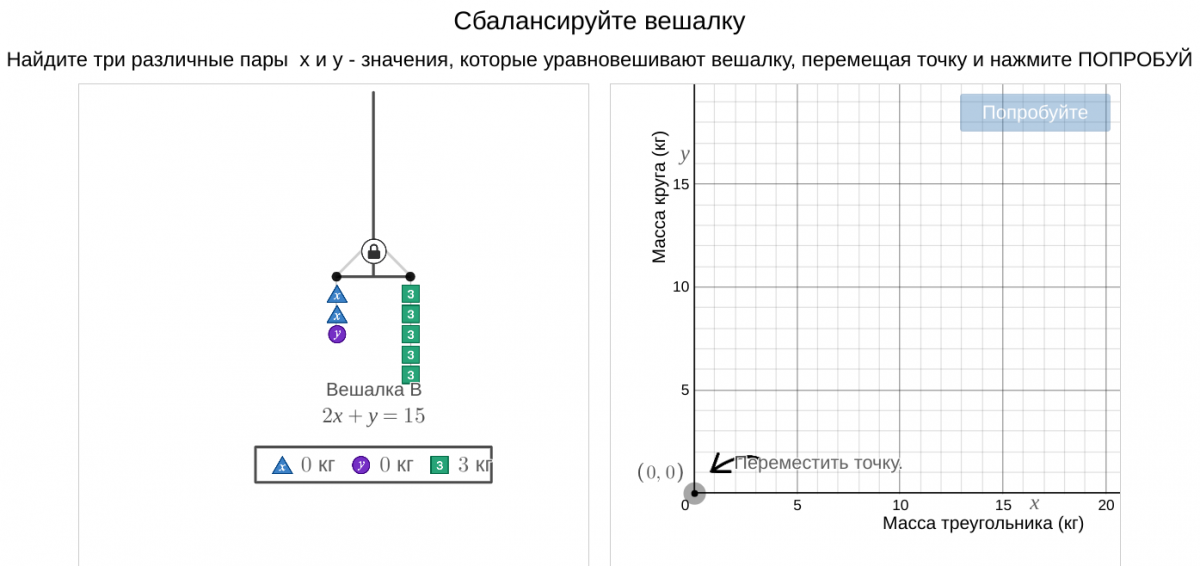
Разберись с балансом (Перевод Натальи Юткиной)
Еще и есть возможность увидеть, как размышляют ученики твоего класса:
Используйте наложение в представлении учителя на приборной панели, чтобы показать распределение ответов. Если позволяет время, подумайте над тем, чтобы задать ученикам следующие вопросы, чтобы помочь им подготовиться к предстоящим заданиям....
Игра, развлечение или серьезная работа?
Как самому создать активность с "вешалками"?
Можно разработать свою собственную активность для отработки навыков решения уравнения при произвольно задаваемых значениях одной из переменных X или Y. Причем проверка правильности решения задания учеником будет осуществляться автоматически.
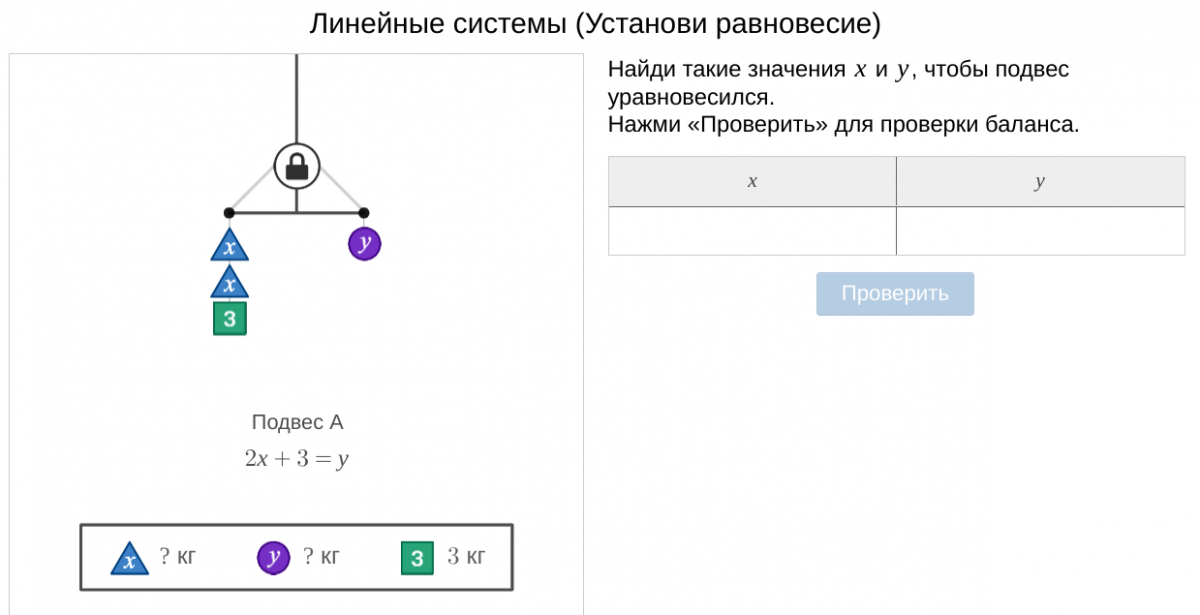
Как из заготовки создать свои слайды?
Чтобы поменять число, порядок и вес каждой фигуры:
- Скопируйте этот слайд в свою активность, используя значок, расположенный рядом с «Предварительным просмотром экрана ученика» в верхнем левом углу слайда.
- Нажмите "Редактировать график".
- Перейдите в папку «Установка» и задайте порядок и количество фигур на каждой стороне подвеса.
- Задайте вес каждой фигуры так, чтобы подвес был сбалансирован.
- Убедитесь, что вы создали разрешимую задачу, используя предварительный просмотр с точки зрения ученика.
- Обновите уравнение, которое должно представлять собой ваш вариант сбалансированного подвеса.
Пример двух кастомизированных слайдов, созданных на основе шаблона по этой инструкции
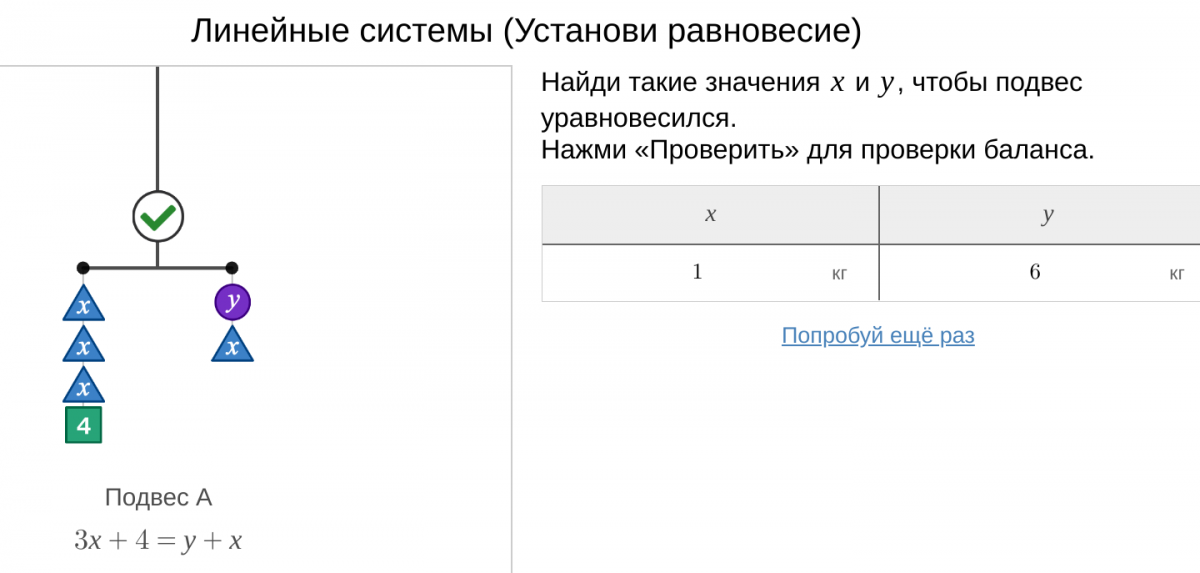
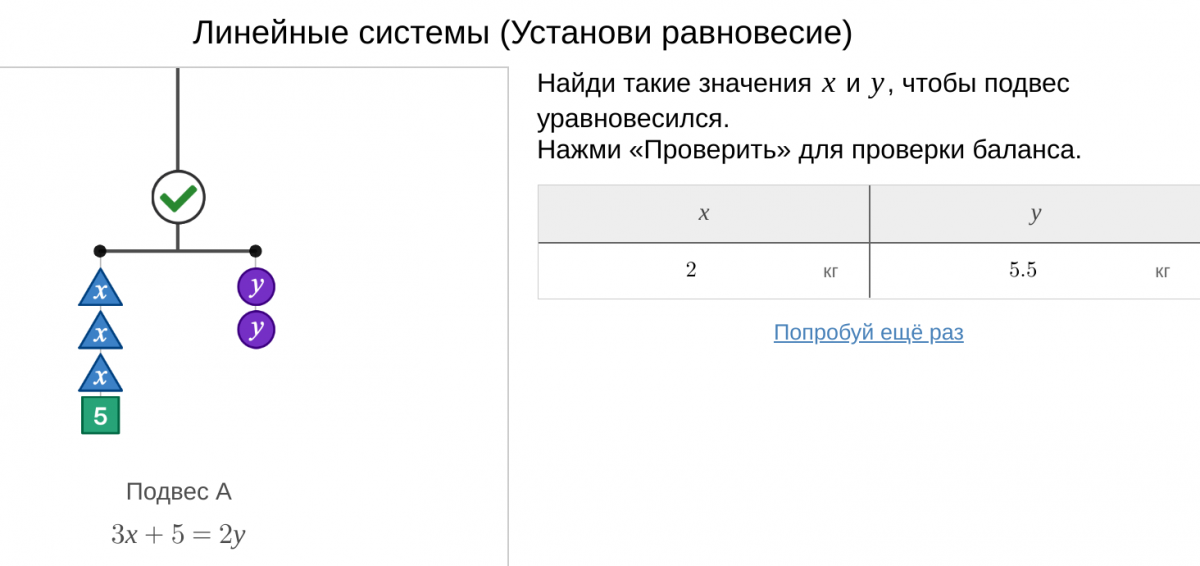
Почему важно менять наше преподавание, если в руках ученика есть такой мощный инструмент, как графический онлайн-калькулятор?
В этом своем посте я пыталась найти ответы на вопрос: как можно по-другому изучать темы линейных уравнений с одной и несколькими переменными, а также темы систем линейных уравнений с двумя переменными? Все это, конечно, с использованием среды Desmos.
А еще заострила бы и, одновременно, обобщила проблему. Нужно ли вообще при изучении темы систем линейных уравнений столько часов на чисто "вычислительные навыки" (все эти "бумажные" методы решения систем), если у учеников страдает представление о моделировании, и, тем более, интерпретации, над которыми мы не работаем как надо. Учитывая, что графический калькулятор Desmos решает графически любую линейную систему в одно мгновение, то есть, от механической рутинной работы нас освобождает.
Остается время на что?
Оставим этот вопрос на обсуждение в сообществе... Ваши версии, коллеги?
Ссылки на публикации по теме
- "Черный ящик" среды цифрового обучения
- Стрельба по мишени, или Цифровые инструменты организации мышления на уроке математики
- Новая стратегия преподавания школьной математики: "умная бумага"
- STEAM-математика: Почему так важны какие-то ползунки?
- Учителям математики нужен новый подход
- Математики больше не плачут, они анализируют проблемы
- Мини-исследование в классе: есть ли у вас чувство времени?
- Стриминговый апрель
-
-
Ускоренный курс по Арт-графике в Desmos: учимся рисовать функциями
- Международный конкурс Арт-математических искусств Desmos
- Идеи заданий с подвижными отрезками
- Виртуальный геоборд своими руками
- От бумаги к цифре: утренние ремиксы
- Мондриан как артефакт
- Ремикс-проект начинается с рамы
- Клетчатая Ёлка и новогодние ремиксы
- Калейдоскопы как ремиксы
- Математическая задача как вызов. Уроки в Desmos
- Инструкция: как создать "объект в зеркале" в среде Desmos
- Курс Desmos-математики стартовал!
- Задачи на оптимизацию — с помощью ползунков Desmos
- О "Розе ветров" и других визуализациях-ремиксах в Desmos
- По следам курса Desmos-математики: бери и делай!
- Polygon: от подвижных геометрических фигур до картин
- Страсть к кругам и окружностям
- Списки? А для чего они нужны? Потренируемся?
- Геометрия "ледяного" узора и принт на футболке
- Классные активности в TeacherDesmos: инструкция для новичка
- Обучение на полиграфе
- Создатели полиграфов
- Мастерская как форма распределенной работы со старшеклассниками: создаем задание в 3D
- Как мы вовлекли учеников в разработку активностей в TeacherDesmos и что из этого вышло
- Необычные коллекции для учителя математики
- Флаги и дроби
- Весы и уравнения
- "Голландский дом" Вермейера как объект для поиска сходств и различий
- Уроки развития 3D-мышления: зачем считать кубики?
- "Недостроенные кубы" для design based learning
- И опять о кубиках: 7 идей развивающих заданий
- Магический квадрат и чудесная лупа
- От бумаги к цифре: домики и клеточки
- Простые математические визуализации - сообща!
- Пляшущие буквы, или шифRуем пRеобRазования!
- Домик Винни Пуха как идея для design based learning
- От узора на клетчатом листке к STEAM-проекту
- От привычки "чатиться" - к математической модели
- Пение сверчка: феномены, процессы, модели
- Данные из текста и карты - в подвижную диаграмму!
- Принцип "четвертый - лишний"
- Мини-исследование в классе: есть ли у вас чувство времени?
- Статистика на карманах
- Все стримы здесь https://www.facebook.com/groups/188977651994702/post_tags/?post_tag_id=537301313828999